���ԍ�
�i���C���C���C���j
�@�@�@�@�@�@�@���� |
��̉����� |
�@�P
�i�P�O�C�P�O�C�R�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�Q�O |
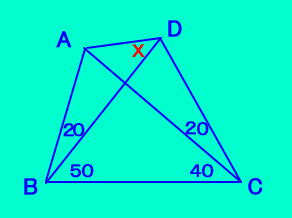
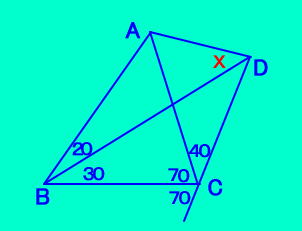
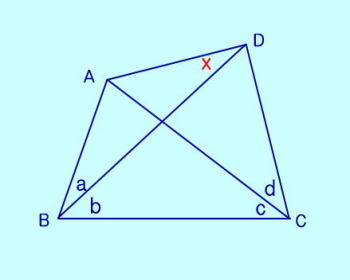
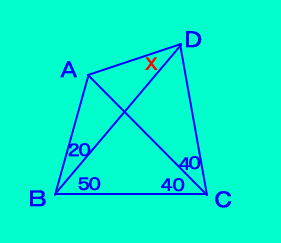
BA��A�̉����Ɂ�ACF=�R�O�ƂȂ�F���Ƃ�Ɠ_E�́�FBC�̓��S�A�l�p�`FBCD�͉~�ɓ��ځA���O�p�`FED�c
|
�Q
�i�P�O�C�P�O�C�R�O�C�P�P�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
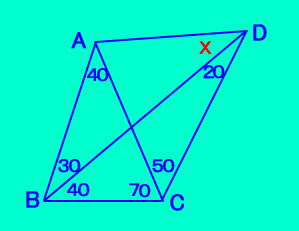
��ABC�̊O�SF���Ƃ�BF,C,D�͓��꒼����ɂ��邱�Ƃ������B�_A�́�BFD�̊O�S�ɂȂ� |
�R�C
�i�P�O�C�P�O�C�S�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�@�R�O |
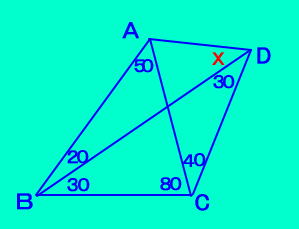
BD�ԂɁ�BAF���Q�O�ƂȂ�_F���Ƃ�ƁA�l�p�`AFCD�͉~�ɓ��ځB��ABF��BF�Ő܂�Ԃ�A��G�Ƃ���Ɓ�AFG�͐��O�p�` |
�S
�i�P�O�C�P�O�C�S�O�C�P�P�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
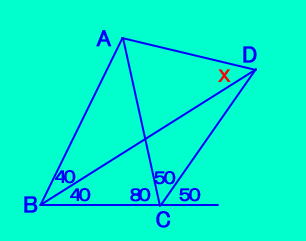
A����BD�ɐ��������낵DC�̌�_��F�ABC�ԂɁ�BAG���Q�O�ƂȂ�G���Ƃ�BG�́�ABF�̊O�S�l�p�`ABFD�̓^�R�`�B |
�T
�i�P�O�C�P�O�C�T�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
�g�s�b�N�X�̖��k�V�Ɠ��l |
�U
�i�P�O�C�P�O�C�T�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�@�Q�O |
��BDC�̓�����BC�̌�_��F�AF�́�ECD�̖T�S�Ł�ABE�߁�FBE�Ŏl�p�`ABFD�̓^�R�`�B |
�V
�i�P�O�C�P�O�C�U�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�S�O |
BA��CD�̌�_��F��DCB�̓�����BA,BD�̌�_��G,H�Ƃ���BH�́�FBC�̓��S�A�l�p�`FGHD,AGCD�͉~�ɓ��ځB |
�W
�i�P�O�C�P�O�C�U�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
BA��CD�̌�_��F�A��AFC�̓����ɐ��O�p�`ACG�ABD�ԂɁ�BCH=�Q�O�ƂȂ�H�A�R�̍����ȎO�p�`���AC=CD���c |
�X
�i�P�O�C�P�O�C�P�O�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�@�V�O |
BD�ԂɁ�BAG=�Q�O�ƂȂ�G,BC�ԂɁ�BAF���S�O�ƂȂ�F���Ƃ�BG�́�ABF�̓��S�B�^�R�`ABFC�A�~�ɓ��ڂ���AGCD�c |
�P�O
�i�P�O�C�P�O�C�P�O�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�@�R�O |
BD�ԂɁ�BAG=�Q�O�A��BAH=�S�O�ƂȂ�G,H���Ƃ�AAH��BC�̌�_��F�Ƃ���BG�́�ABF�̓��S�A�~�ɓ��ڂ���AHCD�c |
�P�P
�i�P�O�C�P�O�C�P�P�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�@�V�O |
�g�s�b�N�X�̖��k�S�Ɠ��l |
�P�Q
�i�P�O�C�P�O�C�P�P�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�@�S�O |
��BCD��BD�Ő܂�Ԃ�C��F�Ƃ���BCA��A�̉�����Ɂ�CDG���P�O�O�ƂȂ�G���Ƃ�B���O�p�`FGD�AFA�͂��̑Ώ̎� |
�P�R
�i�P�O�C�P�O�C�P�Q�O�C�Q�O�j
�@�@�@�@�@�@�@�@�@�@�P�O�O |
��BCD��BD�Ő܂�Ԃ���C��F�Ƃ���B���O�p�`FCD�ƓӎO�p�`FCA�ʼn����B |
�P�S
�i�P�O�C�P�O�C�P�Q�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�@�Q�O |
BC=CD�AAB�ԂɁ�BCF=�Q�O��F���Ƃ�ABF=FC=CA�A��BFC���CD�ɁAA�̔��Α��ɓ\��t���AF��G�AG�́�ACD�̊O�S |
�P�T
�i�P�O�C�P�O�C�P�R�O�C�Q�O�j
�@�@�@�@�@�@�@�@�@�@�P�O�O |
AB�ԂɁ�DCF=�R�O�ƂȂ�F���Ƃ�ƁA�_D�́�FBC�̖T�S�Ł�CFD=�V�O�AE�́�FCD�̊O�S�AD�́�AFE�̊O�S |
�P�U
�i�P�O�C�P�O�C�P�R�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�@�R�O |
��ABC�̊O�SF������B��CFA=�S�O�AFC=CD��聢FCD�͒�p�S�O�̓ӎO�p�`����F,A,D�͓��꒼���� |
�P�V
�i�P�O�C�Q�O�C�Q�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
BA��A�̉�����Ɂ�BCG=�W�O�ƂȂ�G���Ƃ�BE�́�GBC�̊O�S�BGD�͐��O�p�`GEC�̑Ώ̎��A�l�p�`AEDG�͉~�ɓ��ځB |
�P�W
�i�P�O�C�Q�O�C�S�O�C�Q�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
��ABC��BC�Ő܂�Ԃ�A��F�Ƃ���B�l�p�`ABFE�͉~�ɓ��ځBBC��FE�̌�_��G�B�l�p�`EGCD�͉~�ɓ��ځBAG=GD�c |
�P�X
�i�P�O�C�Q�O�C�S�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
BD=BC,BD����ӂƂ��鐳�O�p�`BDF��A�Ƃ͔��Α��ɍ��B���r��`ABFC����A��ABD�߁�FDC |
�Q�O
�i�P�O�C�Q�O�C�S�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
��ABC�̊O�SF�����B�l�p�`BFCD�͓��r��`����A��AFB�߁�ACD����AAB=AD |
�Q�P
�i�P�O�C�Q�O�C�T�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
��ABC��BC�Ő܂�Ԃ��BA��F�Ƃ���B�l�p�`DBFC�͉~�ɓ��ڂ��A��FBD�A��FAD�͓ӎO�p�`�B |
�Q�Q
�i�P�O�C�Q�O�C�T�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
���`�a�b�̊O�S���e�B�`�a�ԂɁڂa�e�g���S�O�̂g���Ƃ�A�`�e�Ƃa�c�̌�_�f�B�g�́��f�a�e�̊O�S���`�g�e�߁��b�f�e�A�`�f�b�c�́c |
�Q�R
�i�P�O�C�Q�O�C�T�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
��ABC��BC�ɂ��Đ܂�Ԃ��BA��F�Ƃ���BD,C,F�͓��꒼����ɂ���A�_A�́�DBF�̊O�S�ɂȂ��Ă���B |
�Q�S
�i�P�O�C�Q�O�C�V�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�S�O |
��ABC�̊O�SF���Ƃ�ABF��AC�̌�_��G�AAF��BD�̌�_��H�A���r��`HFCG�A�~�ɓ��ڂ���l�p�`AHCD�ʼn��� |
�Q�T
�i�P�O�C�Q�O�C�V�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
��ABC�̊O�SF���Ƃ�BF��AC�̌�_��G�AAF��BD�̌�_��H�A���r��`HFCG�ƃ^�R�`AHCD�ʼn����B |
�Q�U
�i�P�O�C�Q�O�C�W�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
���`�a�b�̊O�S�e�͂a�c��ɂ���B�e�b���b�c�A�_�b�́��`�e�c�̊O�S�ɂȂ��Ă���B |
�Q�V
�i�P�O�C�Q�O�C�W�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
���`�a�b�̊O�S�e�͂a�c��ɂ���B���`�e�b�h���O�p�`�œ_�`�́��c�e�b�̊O�S�ɂȂ��Ă���B |
�Q�W
�i�P�O�C�Q�O�C�P�O�O�C�Q�O�j
�@�@�@�@�@�@�@�@�@�@�@�V�O |
�a�c�ԂɁڂa�`�e���P�O�ƂȂ�e���Ƃ�A���`�a�b�̊O�S���f�A���f�a�`�߁��e�a�`�A�~�ɓ��ڂ���l�p�`�`�e�b�c������ |
�Q�X
�i�P�O�C�Q�O�C�P�O�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�@�S�O |
���O�p�`�e�a�b���`���ɍ��ƁA�`�a�͂��̑Ώ̎��A�ڂb�e�`���S�O�A���c�a�b�̊O�S�e���e�C�`�C�c�͓��꒼���� |
�R�O
�i�P�O�C�Q�O�C�P�O�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�@�Q�O |
�g�s�b�N�X�̖��k�X |
�R�P
�i�P�O�C�Q�O�C�P�P�O�C�Q�O�j
�@�@�@�@�@�@�@�@�@�@�V�O |
���`�a�b���`�a�Ő܂�Ԃ��B�b���e�Ƃ���B�e�́��c�a�b�̊O�S�A�^�R�`�`�e�a�b�ƁA�~�ɓ��ڂ���l�p�`�`�e�a�c�ʼn����B |
�R�Q
�i�P�O�A�Q�O�A�P�P�O�A�R�O�j
�@�@�@�@�@�@�@�@�@�@�@�R�O |
���`�a�b���`�a�Ő܂�Ԃ��A�b���e�Ƃ���B�^�R�`�`�e�a�b���ڂ`�e�b���T�O�A���e�a�c�̊O�S�b����A�e�C�`�C�c�͓��꒼����B |
�R�R
�i�P�O�C�Q�O�C�P�P�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
���c�a�b�̊O�S�e�A���`�a�b�̊O�S�f�����B�^�R�`�e�f�b�`���`�e�͐��O�p�`�e�a�c�̑Ώ̎��ɂȂ�B�`�a���`�c |
�R�S
�i�P�O�C�Q�O�C�P�R�O�C�Q�O�j
�@�@�@�@�@�@�@�@�@�@�@�R�O |
���a�b�c�̊O�S�e�����B�ڂa�e�b���ڂa�`�b����~�ɓ��ڂ���l�p�`�e�a�b�`�B�`�c�͐��O�p�`�e�a�c�̑Ώ̎��B |
�R�T
�i�P�O�C�R�O�C�Q�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
���c�a�b�̊O�S�e���Ƃ��A�a�e�Ƃ`�b�̌�_���f�A�`�f�͐��O�p�`�c�e�b�̑Ώ̎�����A�ڂ`�f�a���ڂ`�f�c�A�l�p�`�`�a�f�c�́c |
�R�U
�i�P�O�C�R�O�C�R�O�C�Q�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
�`�b�̂b�̉����Ɂڂc�e�`���P�O�ƂȂ�e���Ƃ�A���c�a�b�̊O�S�f���Ƃ�B�a�C�f�C�e�����꒼����������A�l�p�`�`�a�e�c�́c |
�R�V
�i�P�O�C�R�O�C�R�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
�g�s�b�N�X�̖��k�U�Ɠ��l |
�R�W
�i�P�O�C�R�O�C�S�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
���a�b�c���a�b�Ő܂�Ԃ��A�c���e�Ƃ���B�l�p�`�`�a�e�b�͉~�ɓ��ڂ���B���`�a�e���`�c�e�͓ӎO�p�`�c |
�R�X
�i�P�O�C�R�O�C�U�O�C�Q�O�j
�@�@�@�@�@�@�@�@�@�@�S�O |
���c�a�b�̊O�S�e�Ƃ��A�a�e�Ƃ`�b�̌�_���g�Ƃ���B�l�p�`�`�a�g�c�̓^�R�`�B�c�g�͐��O�p�`�c�e�b�̑Ώ̎� |
�S�O
�i�P�O�C�R�O�C�U�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
���a�b�c���a�c�Ő܂�Ԃ��b���e�Ƃ���B�a�`�Ƃe�c�̌�_���f�B�e�a�b�f�͉~�ɓ��ځB�l�p�`�f�`�b�c�̓^�R�`�������B |
�S�P
�i�P�O�C�R�O�C�V�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
�b�Ɣ��Α��ɐ��O�p�`�`�a�e�����e�b�Ƃa�c�̌�_���g�Ƃ���B�a�́��`�e�b�́A�e�́��`�a�g�̊O�S�A�l�p�`�`�g�b�c�́c |
�S�Q
�i�P�O�C�R�O�C�V�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
���d�a�b�̊O�S�e�Ƃ��A�d�c���d�e���a�e�A���d�e�c�߁��e�a�b����A�`�a���e�c�A���s�l�ӌ`�`�a�e�c�ƂȂ�B |
�S�R
�i�P�O�C�R�O�C�W�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
���c�a�b�̊O�S�e�A�`�b�͐��O�p�`�c�e�b�̑Ώ̎��ł`�e���`�c�A�^�R�`�łe�`���`�f���A�`�́��e�c�f�̊O�S�A�ڂe�c�f���Q�O�c |
�S�S
�i�P�O�C�R�O�C�W�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
�`����b�c�ɐ��������낵�a�b�̌�_���e�B�`�a���a�b�A�`�b���b�e�A�c�̔��Α��ɐ��O�p�`�`�e�f�����B�`�́��a�f�c�̊O�S |
�S�T
�i�P�O�C�R�O�C�P�O�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�@�Q�O |
���c�a�b�̊O�S�e�B�`�b�͐��O�p�`�e�b�c�̑Ώ̎��B�~�ɓ��ڂ���l�p�`�`�e�a�b���A�ڂ`�e�b���ڂ`�c�b���S�O |
�S�U
�i�P�O�C�R�O�C�P�P�O�C�Q�O�j
�@�@�@�@�@�@�@�@�@�@�@�S�O |
���a�b�c���a�c�Ő܂�Ԃ��A�b���e�Ƃ���B�e�́��`�a�b�̊O�S�B�ڂe�`�a���ڂe�c�a����~�ɓ��ڂ���l�p�`�`�e�a�c |
�S�V
�i�P�O�C�R�O�C�P�P�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
���`�a�b�̊O�S�e�����B�ڂ`�e�b���W�O�B�^�R�`�e�a�b�c����A�ڂb�e�c���W�O����A�e�C�`�C�c�C�͓��꒼���� |
�S�W
�i�P�O�C�R�O�C�P�Q�O�C�Q�O�j
�@�@�@�@�@�@�@�@�@�@�@�Q�O |
���a�b�c�̊O�S�e�A�ڂa�e�b���ڂa�`�b����A�`�e�a�b�͉~�ɓ��ځB�`�e���`�b����A�`�c�͐��O�p�`�c�e�b�̑Ώ̎� |
�S�X
�i�P�O�C�S�O�C�R�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
�a�c���a�b�A���O�p�`�e�a�b���c���ɍ��A�b�`�͂��̑Ώ̎��B���d�a�`�߁��c�a�`���A�ڂ`�d�a���P�O |
�T�O
�i�P�O�C�S�O�C�T�O�C�Q�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
�`�a���`�b�A���O�p�`�e�a�b���c���ɍ��ƁA�`�e�͂��̑Ώ̎��B�a�b���a�c�A���`�e�a�߁��`�c�a |
�T�P
�i�P�O�C�S�O�C�T�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
���O�p�`�`�b�e���c���ɍ��B�b�c�͂��̑Ώ̎��ł`�c���c�e�B�`�b�Ƃa�e�̌�_���f�A�^�R�`�c�`�a�f����`�c���c�f�A�c�͊O�S�c |
�T�Q
�i�P�O�C�S�O�C�W�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
���`�b�c���`�b�Ő܂�Ԃ��c���e�Ƃ���B�ڂa�`�b���ڂa�e�b���e�a�b�`�͉~�ɓ��ځA�ڂ`�e�b���ڂ`�a�b |
�T�R
�i�P�O�C�S�O�C�W�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
���O�p�`�`�b�e���c���ɍ��B�a�c�V�b�d�B�ڂe�a�b���ڂa�e�b���ڂc�a�e����A���r��`�c�a�b�e�c�`�a���`�c |
�T�S
�i�P�O�C�S�O�C�P�O�O�C�Q�O�j
�@�@�@�@�@�@�@�@�@�@�@�R�O |
�c�a�ԂɁڂa�`�e���P�O�̂e���Ƃ�Ɠ��r��`�`�e�b�c�B���`�a�b�̊O�S�f�B���f�a�`�߁��e�a�`�ła�e���a�b |
�T�T
�i�P�O�C�V�O�C�S�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
�c�a���c�b�A�a���ɐ��O�p�`�c�b�e�����B�a�`�Ƃe�c�̌�_���f�Ƃ���B���c�a�f�߁��e�b�a�A�a�f���a�b�A�f�c�b�`�͉~�ɓ��ځB |
�T�U
�i�P�O�C�V�O�C�T�O�C�Q�O�A�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
�a�b���b�c�A�`���ɐ��O�p�`�b�c�e�����B���`�a�b�߁��`�e�b�߁��`�e�c |
�T�V
�i�P�O�C�V�O�C�T�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
�g�s�b�N�X�̖��k�P�X |
�T�W
�i�P�O�C�V�O�C�U�O�C�Q�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
���a�c�b�̊O�S���e�͂`�b��A���`�a�b�̓��S�f�A�f�b�͐��O�p�`�e�a�b�̑Ώ̎��łc�C�e�C�f�͓��꒼����A�`�f�b�c�͉~�Ɂc |
�T�X
�i�P�O�C�P�O�O�C�R�O�C�Q�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
���c�a�b�̊O�S�e�B�`�b�͐��O�p�`�e�a�b�̑Ώ̎��B���`�a�e�߁��`�e�c |
�U�O
�i�P�O�C�P�O�O�C�S�O�C�Q�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
���`�a�b�̊O�S�e���Ƃ�ƁA�a�́��e�d�b�̊O�S�ڂe�d�b���ڂe�a�b�^�Q���R�O�A�ڂe�`�d���ڂe�c�d�Ŏl�p�`�c�`�d�e�͉~�ɓ��� |
�U�P
�i�Q�O�C�P�O�C�Q�O�C�P�Q�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
���a�c�b�̊O�S�e�����B�`�a�͐��O�p�`�e�a�b�̑Ώ̎��B�ڂ`�e�c�{�ڂ`�b�c���P�W�O�łe�`�b�c�͉~�ɓ��ڂ���B |
�U�Q
�i�Q�O�C�P�O�C�S�O�C�U�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
���Q�P�ԂƓ��l |
�U�R
�i�Q�O�C�P�O�C�S�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
���Q�R�ԂƓ��l |
�U�S
�i�Q�O�C�P�O�C�S�O�C�P�Q�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
�a�b���b�c�A�`���ɐ��O�p�`�a�b�e�����Ƃb�́��e�a�c�̊O�S�B�`�a�́��a�b�e�̑Ώ̎��B�l�p�`�e�`�b�c�͉~�ɓ��ځB |
�U�T
�i�Q�O�C�P�O�C�T�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�S�O |
���`�a�b�̊O�S�e�B�a�c�V�e�b�B�e���`�a�ɐ��������낵�A�a�c�̌�_�f�B�ڂf�e�b���ڂe�b�c�œ��r��`�B���`�e�f�߁��`�b�c |
�U�U
�i�Q�O�C�P�O�C�T�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
���a�b�c�̊O�S�e�Ƃ���B���a�e�`�߁��e�c�b�B���e�b�c�̒��ɐ��O�p�`�b�c�f�����B���f�b�e�߁��`�e�c |
�U�V
�i�Q�O�C�P�O�C�T�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�@�Q�O |
���Q�O�ԂƓ��l |
�U�W
�i�Q�O�C�P�O�C�V�O�C�V�O�j
�@�@�@�@�@�@�@�@�@�@�S�O |
���Q�V�ԂƓ��l |
�U�X
�i�Q�O�C�P�O�C�V�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
���Q�U�ԂƓ��l |
�V�O
�i�Q�O�C�P�O�C�W�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�U�O |
���a�b�c���a�c�Ő܂�Ԃ��B�b���e�Ƃ��A�c�e�Ƃ`�a�̌�_�f�A���f�a�c�̓��S�g�Ƃ���B���`�f�e�߁��g�f�e�Ń^�R�`�`�f�g�c�B |
�V�P
�i�Q�O�C�P�O�C�W�O�C�U�O�j
�@�@�@�@�@�@�@�@�@�@�T�O |
���Q�X�ԂƓ��l |
�V�Q
�i�Q�O�C�P�O�C�P�O�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�@�W�O |
�ڂ`�a�d�̓����Ƃ`�b�̌�_�e�A�`�c�Ƃ̌�_�g�Ƃ���B�c�́��e�a�b�̖T�S�Łڂc�e�b���U�O�A���`�a�e�߁��c�a�e |
�V�R
�i�Q�O�C�P�O�C�P�O�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�@�U�O |
���R�R�ԂƓ��l |
�V�S
�i�Q�O�C�P�O�C�P�O�O�C�U�O�j
�@�@�@�@�@�@�@�@�@�@�@�R�O |
���R�Q�ԂƓ��l |
�V�T
�i�Q�O�C�P�O�C�P�P�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�P�O�O |
���a�b�c�̊O�S�e�ł`�a�́��e�a�b�̑Ώ̎��B�ڂe�`�b���ڂe�c�b���`�e�b�c�͉~�ɓ��� |
�V�U
�i�Q�O�C�P�O�C�P�P�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�@�W�O |
���a�b�c���a�c�Ő܂�Ԃ��B�b���e�Ƃ���B�ڂe�d�a���U�O���e�́��`�a�d�̓��S�B���a�e�`�߁��a�e�c |
�V�V
�i�Q�O�C�P�O�C�P�P�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�@�S�O |
�`���ɐ��O�p�`�a�b�e�����B�a�b���b�c�C�`�a�́��e�a�b�́A�`�b�́��e�b�c�̑Ώ̎� |
�V�W
�i�Q�O�C�P�O�C�P�R�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�P�O�O |
�c�̔��Α��ɐ��O�p�`�`�d�e�����B�`�d���d�a�A�e�a�b�d�͉~�ɓ��ڂ��A�e�b�ۂa�c�A�e�a���e�c�A�ڂe�c�d���T�O�A�^�R�`�e�d�c�`�c |
�V�X
�i�Q�O�C�Q�O�C�R�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
�g�s�b�N�X�̖��k10 |
�W�O
�i�Q�O�C�Q�O�C�R�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
���c�a�b�̊O�S�e�����B�`�b�́��e�a�b�̑Ώ̎��B�ڂc�e�b���ڂ`�e�b���S�O�A�ڂ`�b�c���P�O�O�ŁA�l�p�`�e�`�b�c�͉~�ɓ��� |
�W�P
�i�Q�O�C�Q�O�C�S�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
�g�s�b�N�X�̖��k�V |
�W�Q
�i�Q�O�C�Q�O�C�S�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
���U�ԂƓ��l |
�W�R
�i�Q�O�C�Q�O�C�P�O�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�@�W�O |
�g�s�b�N�X�̖��k�S |
�W�S
�i�Q�O�C�Q�O�C�P�O�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�@�Q�O |
���T�R�ԂƓ��l |
�W�T
�i�Q�O�C�Q�O�C�P�P�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�@�W�O |
���`�a�b�̊O�S�e���Ƃ�ƁA�b�́��a�e�c�̊O�S�A���e�a�`�߁��b�a�c�ł`�a���a�c |
�W�U
�i�Q�O�C�Q�O�C�P�P�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�@�R�O |
���P�O�ԂƓ��l |
�W�V
�i�Q�O�C�R�O�C�Q�O�D�U�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
���R�W�ԂƓ��l |
�W�W
�i�Q�O�C�R�O�C�R�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
�g�s�b�N�X�̖��k�U |
�W�X
�i�Q�O�C�R�O�C�R�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
�a�`�̂`�̉�����Ɂڂa�b�e���V�O�ƂȂ�e�A�e�b�Ƃa�c�̌�_�f�Ƃ���B�e�`�d�f�͉~�ɓ��ځA�d�́��e�a�b�́A�f�́��`�c�b�̊O�S |
�X�O
�i�Q�O�C�R�O�C�T�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�S�O |
�c���ɁA���O�p�`�`�b�e�����B�`�a���`�b�A���`�a�e���a�C�c�C�e�͓��꒼����B�c�b�́��`�b�e�̑Ώ̎� |
�X�P
�i�Q�O�C�R�O�C�T�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
�a�c��Ɂڂ`�b�e���U�O�ƂȂ�e���Ƃ�ƁA�`�́��e�a�b�̊O�S�܂��A�e�́��`�b�c�̊O�S |
�X�Q
�i�Q�O�C�R�O�C�W�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�U�O |
�`�b���b�a�A�`���ɐ��O�p�`�e�a�b�����B�a�c�͂��̑Ώ̎��ڂe�`�b���ڂe�c�b����A�`�c�b�e�͉~�ɓ��ڂ���B |
�X�R
�i�Q�O�C�R�O�C�W�O�C�U�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
�a�b���`�b�A�`���ɐ��O�p�`�e�a�b�����B�a�c�͂��̑Ώ̎�����A�ڂc�e�b���W�O�A�b�́��`�e�a�̊O�S����A�ڂ`�e�b���W�O |
�X�S
�i�Q�O�C�R�O�C�P�O�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�@�U�O |
���`�a�b�̊O�S�e�A�܂��e�͂b�̂a�c�ɂ��Ă̑Ώ̓_�B�ڂe�`�b���ڂe�c�b���l�p�`�`�e�b�c�͉~�ɓ��ڂ���B |
�X�T
�i�Q�O�C�R�O�C�P�O�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�@�Q�O |
���S�U�ԂƓ��l |
�X�U
�i�Q�O�C�R�O�C�P�P�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�@�S�O |
���S�T�ԂƓ��l |
�X�V
�i�Q�O�C�S�O�A�Q�O�A�T�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
���P�X�ԂƓ��l |
�X�W
�i�Q�O�C�S�O�C�S�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
�g�s�b�N�X�̖��k�P�S |
�X�X
�i�Q�O�C�S�O�C�S�O�C�V�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
�b�`�̉�����Ɂڂ`�a�e���Q�O�ƂȂ�e���Ƃ�B�c�́��e�a�b�̖T�S�܂��A�`�́��e�a�c�̓��S |
�P�O�O
�i�Q�O�C�S�O�C�W�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�T�O |
���a�c�b���a�c�Ő܂�Ԃ��A�b���e�Ƃ���B�`�́��e�a�d�̖T�S�ŁA�ڂe�`�a���R�O�D�`�b�́��e�c�b�̑Ώ̎� |
�P�O�P
�i�Q�O�C�S�O�C�W�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
�g�s�b�N�X�̖��k�X�Ɠ��l |
�P�O�Q
�i�Q�O�C�S�O�C�P�O�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�@�R�O |
�a�c�ԂɁڂc�b�e���P�O�̂e���Ƃ�ƁA�b�d���d�e���e�`�A���d�b�e���b�e���e�c���灢�`�e�c�̒��ɓ\��t����B���O�p�`�̒��_���O�S |
�P�O�R
�i�Q�O�C�T�O�C�S�O�C�U�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
���`�a�b���`�b�Ő܂�Ԃ��B�a���e�B�b�e�Ƃa�`�̌�_���f�B�f�a�b�c�͉~�ɓ��ڂ���B���f�`�e�̊O�S�g�Ł��g�e�f�߁��c�e�f |
�P�O�S
�i�Q�O�C�T�O�C�V�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�S�O |
���T�Q�ԂƓ��l |
�P�O�T
�i�Q�O�C�U�O�C�R�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
�g�s�b�N�X�̖��k�P�V |
�P�O�U
�i�Q�O�C�U�O�C�T�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
�g�s�b�N�X�̖��k�P�P |
�P�O�V
�i�Q�O�C�U�O�C�T�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
�a�`�̉�����Ɂڂa�c�e���W�O�ƂȂ�e���Ƃ�Ɠ��r��`�e�a�b�c�B���e�a�c�̒��ɐ��O�p�`�e�c�g�����B���`�a�c�߁��g�c�a |
�P�O�W
�i�Q�O�C�U�O�C�V�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
�b���ɐ��O�p�`�`�a�e�����B�`�b�͂��̑Ώ̎��B�c�a�b�e�͉~�ɓ��ڂ���B�c�e���e�`���e�a����A�e�́��`�a�c�̊O�S |
�P�O�X
�i�Q�O�C�W�O�C�R�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
���a�b�c�̊O�S�e���Ƃ�B�`�b�͐��O�p�`�e�a�b�̑Ώ̎��B�ڂ`�e�c���ڂ`�e�b���A���`�e�c�߁��`�e�b�ł`�b���`�c |
�P�P�O
�i�Q�O�C�W�O�C�S�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
�g�s�b�N�X�̖��k�P�X�Ɠ��l |
�P�P�P
�i�Q�O�C�W�O�C�S�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
���T�U�ԂƓ��l |
�P�P�Q
�i�Q�O�C�W�O�C�T�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
���`�a�b�̊O�S�e�����B�`�e�Ƃc�b�̌�_���f�A�^�R�`�e�a�b�f�̑Ώ̎��a�f����A�ڂe�a�f���R�O�A�ӎO�p�`�`�a�f |
�P�P�R
�i�Q�O�C�P�O�O�C�Q�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
�`���܂ސ��O�p�`�c�e�b�����B�c�a�Ƃe�b�̌�_�l�A�ڂe�a�l���ڂ`�a�e�A�ڂ`�d�e���ڂe�d�a�łe�́��`�d�a�̖T�S�B�ڂ`�e�d���P�O |
�P�P�S
�i�Q�O�C�P�O�O�C�S�O�C�R�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
�c�b��Ɂڂb�a�e���S�O�ƂȂ�e���Ƃ�B���O�p�`�d�a�e�A���d�`�e�͒�p�P�O�̓ӎO�p�`�łc�`�d�e�͉~�ɓ��ڂ���B |
�P�P�T
�i�R�O�C�P�O�C�Q�O�C�P�R�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
���a�b�c�̊O�S���e�A�e�b�Ƃa�`�̌�_���f�B�a�f�͐��O�p�`�e�a�c�̑Ώ̎��B�`�́��f�b�c�̖T�S����A�ڂf�c�`���R�O |
�P�P�U
�i�R�O�C�P�O�C�R�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�@�Q�O |
���`�a�b�̊O�S���e�B�a�c�͐��O�p�`�`�a�e�̑Ώ̎�����ڂ`�c�a���ڂa�c�e�A�a�e�b�c�͉~�ɓ��ڂ���̂ŁA�ڂa�c�e���Q�O |
�P�P�V
�i�R�O�C�P�O�C�R�O�C�P�R�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
�a�b���b�c�A�`���ɐ��O�p�`�e�b�c�����B���a�b�e����A�a�C�`�C�e�͓��꒼����B�`�e���e�b���e�c����e�́��`�b�c�̊O�S�B |
�P�P�W
�i�R�O�A�P�O�C�S�O�C�P�P�O�j
�@�@�@�@�@�@�@�@�@�@�@�Q�O |
���a�b�c�̊O�S���e�A�a�`�͐��O�p�`�e�a�c�̑Ώ̎��B�`�e�́��e�a�b�Ɓ��`�a�b�̑Ώ̎��B�ڂa�e�`���ڂ`�e�b���ڂ`�c�a |
�P�P�X
�i�R�O�C�P�O�C�U�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�S�O |
���a�b�c�̊O�S�e�����B�e�c�ԂɁڂe�b�f���U�O�ƂȂ�f���Ƃ�ƁA���e�a�`�߁��b�e�c�ł`�e���b�f���b�c�A���O�p�`�b�c�g�����c |
�P�Q�O
�i�R�O�C�P�O�C�U�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�@�Q�O |
�a�b���b�c�A�`���ɐ��O�p�`�e�b�c�����B�ӎO�p�`�e�a�b����A�a�C�`�C�e�͓��꒼����`�e���`�b����A�^�R�`�`�b�c�e |
�P�Q�P
�i�R�O�C�P�O�C�V�O�C�V�O�j
�@�@�@�@�@�@�@�@�@�@�T�O |
���a�c�b�̊O�S�e���Ƃ�ƁA�ڂc�e�b���Q�O�B�a�`���a�b���a�e�Ł��`�a�e���ڂ`�e�b���Q�O�@����Ăe�C�`�C�c�͓��꒼����A |
�P�Q�Q
�i�R�O�C�P�O�C�V�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�S�O |
���a�b�c�̊O�S���e�Ƃ���ƁA�ڂb�e�c���Q�O�A�`�a�͐��O�p�`�e�a�c�̑Ώ̎����A�ڂ`�c�a���ڂ`�e�a |
�P�Q�R
�i�R�O�C�P�O�C�W�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�V�O |
�b���ɐ��O�p�`�`�a�e�����B�a�e�̒��_�l�A�`�l�Ƃa�b�̌�_�m�Ƃ��A�a�c�A�`�l�͂��̑Ώ̎��B���c�b�m�߁��c�b�e�A�c�͊O�S�c |
�P�Q�S
�i�R�O�C�P�O�C�W�O�C�V�O�j
�@�@�@�@�@�@�@�@�@�@�T�O |
���a�b�c�̊O�S�e�Ƃ���ƁA�a�`�͐��O�p�`�e�a�c�̑Ώ̎��B�b�`�Ƃe�c�̌�_�f�B�l�p�`�e�a�`�f�͉~�ɓ��ڂ���B |
�P�Q�T
�i�R�O�C�P�O�C�P�O�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�@�W�O |
���a�b�c�̊O�S�e���Ƃ�B�a�`�͐��O�p�`�e�a�c�̑Ώ̎��B�l�p�`�e�a�b�`�͉~�ɓ��ڂ���B |
�P�Q�U
�i�R�O�C�P�O�C�P�P�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�P�O�O |
�d���܂ސ��O�p�`�`�a�e�����B�`�d�C�a�d�͂��̑Ώ̎��B�d�͏d�S����A�ڂc�d�e���ڂb�d�e�ŁA�e�́��b�d�c�̖T�S�ɂȂ�B |
�P�Q�V
�i�R�O�C�P�O�C�P�P�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�@�V�O |
�g�s�b�N�X�̖��k�P�X�Ɠ��l |
�P�Q�W
�i�R�O�C�P�O�C�P�Q�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�P�O�O |
���S�P�ԂƓ��l |
�P�Q�X
�i�R�O�C�Q�O�C�Q�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
�`�̔��Α��ɐ��O�p�`�c�b�e�����B���`�a�b�̊O�S�g�Ƃ���B���a�d�b�߁��a�g�b�A���`�g�b�߁��d�b�c�A���c�d�e�߁��b�`�c |
�P�R�O
�i�R�O�C�Q�O�C�R�O�C�V�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
���a�b�c�̊O�S�e�͂`�b��a�`�̂`�̉�����Ɂڂe�f�a���Q�O�̂f���Ƃ�ƁA�e�́��f�a�c�̊O�S�A�f�́��`�e�c�̊O�S |
�P�R�P
�i�R�O�C�Q�O�C�R�O�C�P�P�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
���P�P�U�ԂƓ��l |
�P�R�Q
�i�R�O�C�Q�O�C�T�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�S�O |
�`�a���`�b�A�b���ɐ��O�p�`�`�a�e�����B�a�c�͂��̑Ώ̎��Łڂ`�c�a���ڂe�c�a�A�ڂ`�b�e���W�O�A�c�́��d�e�b�̖T�S�B |
�P�R�R
�i�R�O�C�Q�O�C�T�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
���P�P�W�ԂƓ��l |
�P�R�S
�i�R�O�C�Q�O�C�W�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�V�O |
�a�b���`�b�A�c���܂ސ��O�p�`�`�b�e�����B���b�a�e����A�a�C�c�C�e�͓��꒼����B�c�b���c�e����`�c�͑Ώ̎��B |
�P�R�T
�i�R�O�C�Q�O�C�W�O�C�V�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
���P�Q�Q�ԂƓ��l |
�P�R�U
�i�R�O�C�Q�O�C�P�O�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�@�W�O |
�g�s�b�N�X�̖��k�P�X�Ɠ��l |
�P�R�V
�i�R�O�C�Q�O�C�P�O�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�@�S�O |
���P�O�O�ԂƓ��l |
�P�R�W
�i�R�O�C�Q�O�C�P�P�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�@�V�O |
���P�Q�T�ԂƓ��l |
�P�R�X
�i�R�O�C�S�O�C�R�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
�g�s�b�N�X�̖��k�P�T |
�P�S�O
�i�R�O�C�S�O�C�R�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
���a�b�c�̊O�S�e�Ƃ���B�`�b�́��e�a�b�̑Ώ̎��B�ڂ`�e�c���P�T�O�A�ڂ`�a�c���R�O�Ŏl�p�`�`�a�c�e�͉~�ɓ��ڂ���B |
�P�S�P
�i�R�O�C�S�O�C�S�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
�g�s�b�N�X�̖��k�P�Q |
�P�S�Q
�i�R�O�C�S�O�C�V�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�T�O |
���P�R�Q�ԂƓ��l |
�P�S�R
�i�R�O�C�S�O�C�W�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�T�O |
���P�O�O�ԂƓ��l |
�P�S�S
�i�R�O�C�S�O�C�W�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
���T�Q�ԂƓ��l |
�P�S�T
�i�R�O�C�T�O�C�R�O�C�V�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
���R�T�ԂƓ��l |
�P�S�U
�i�R�O�C�T�O�C�S�O�C�V�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
�a�d�ԂɁڂd�`�e���Q�O�@�̂e���Ƃ�ƁA�`�e�b�c�͉~�ɓ��ڂ���B���`�a�d�̊O�S�f���Ƃ�A�`�f�a�b�͉~�ɓ��ځB���`�e�b�߁��f�e�b�c |
�P�S�V
�i�R�O�C�T�O�C�U�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�S�O |
���c�a�b�̊O�S�e�Ƃ���B�c�e�Ƃ`�a�̌�_�f�Ƃ���B�^�R�`�f�a�b�e�Ɖ~�ɓ��ڂ���l�p�`�`�f�b�c�ʼn��� |
�P�S�W
�i�R�O�C�T�O�C�V�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�S�O |
�g�s�b�N�X�̖��k�P�U |
�P�S�X
�i�R�O�C�V�O�C�Q�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
�a�c���c�b�A�`���܂ސ��O�p�`�e�a�c�����ƁA�`�a�͑Ώ̎��ɂȂ�B�e�b�Ƃ`�a�̌�_�f�Ƃ���ƁD�c�f�`�b�͉~�ɓ��ڂ���B |
�P�T�O
�i�R�O�C�V�O�C�R�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
���X�O�ԂƓ��l |
�P�T�P
�i�R�O�C�V�O�C�T�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
�g�s�b�N�X�̖��k�U�Ɠ��l |
�P�T�Q
�i�R�O�C�V�O�C�U�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
���c�a�b�̊O�S�e�A�e�b�Ƃa�c�̌�_�f�A�c�e�Ƃ`�b�̌�_�g�Ƃ���B�f�́��g�c�b�̓��S�B�`�a�b�e�͉~�ɓ��ځB���`�e�g�߁��f�e�g |
�P�T�R
�i�R�O�C�W�O�C�R�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
���X�O�ԂƓ��l |
�P�T�S
�i�R�O�C�W�O�C�S�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
�g�s�b�N�X�̖��k�S�Ɠ��l |
�P�T�T
�i�R�O�C�P�O�O�C�Q�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
�d���܂ސ��O�p�`�`�a�e�����B�`�b�Ƃa�c�͂��̑Ώ̎��ɂȂ��Ă���B�e�́��c�d�b�̓��S |
�P�T�U
�i�R�O�C�P�O�O�C�R�O�C�S�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
���`�a�b�̊O�S�e�͂c�b��ŁA�a�c�͐��O�p�`�`�a�e�̑Ώ̎� |
�P�T�V
�i�S�O�C�P�O�C�R�O�C�P�P�O�j
�@�@�@�@�@�@�@�@�@�@�@�Q�O |
���W�O�ԂƓ��l |
�P�T�W
�i�S�O�C�P�O�C�T�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�@�R�O |
�`�a���`�b�A�b���ɐ��O�p�`�`�a�e�����B���`�e�b���A�e�C�b�C�c�͓��꒼����B�a�e���e�c���`�e |
�P�T�X
�i�S�O�C�P�O�C�T�O�C�P�P�O�j
�@�@�@�@�@�@�@�@�@�@�@�Q�O |
�a�b���b�c�C�`���ɐ��O�p�`�e�b�c�����B�`�b��Ώ̎��ɂ���^�R�`�`�a�b�e�ƃ^�R�`�`�b�c�e�ʼn����B |
�P�U�O
�i�S�O�C�P�O�C�W�O�C�U�O�j
�@�@�@�@�@�@�@�@�@�@�V�O |
�`�b���a�b�A�`���ɐ��O�p�`�e�a�b�����B�ڂa�e�`���ڂa�b�c�Ł��e�a�`�߁��b�a�c�A�`�a���c�a |
�P�U�P
�i�S�O�C�P�O�C�W�O�C�V�O�j
�@�@�@�@�@�@�@�@�@�@�U�O |
���`�c�b���`�b�Ő܂�Ԃ��B�c���e�Ƃ���B�`�b���b�a����A���e�a�b�����`�b�e�̒��ɂ͂����e���f�Ƃ���B���O�p�`�e�b�f�c |
�P�U�Q
�i�S�O�C�P�O�C�P�O�O�C�U�O�j
�@�@�@�@�@�@�@�@�@�@�@�V�O |
���W�T�ԂƓ��l |
�P�U�R
�i�S�O�C�Q�O�C�Q�O�C�P�P�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
���a�b�c�̊O�S�e�Ƃ���ƁA�a�c�Ƃe�b�̌�_�f�Ƃ���ƁA���e�a�b�C���e�`�f�͐��O�p�`�B�`�f���f�e���f�c |
�P�U�S
�i�S�O�C�Q�O�C�S�O�C�V�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
���a�b�c�̊O�S�e�B�b���ɐ��O�p�`�a�e�f�����B���`�e�f�߁��`�e�c�B�`�a���a�e����A�a�́��`�e�f�̊O�S |
�P�U�T
�i�S�O�C�Q�O�C�S�O�C�P�P�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
���a�b�c�̊O�S���e�A�a�`�Ƃe�b�̌�_���f�Ƃ���B�e�f���a�f����A�f�c�́��e�a�c�̑Ώ̎��B�^�R�`�f�`�b�c�`�����B |
�P�U�U
�i�S�O�C�Q�O�C�W�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�V�O |
���V�Q�ԂƓ��l |
�P�U�V
�i�S�O�C�Q�O�C�W�O�C�V�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
���a�b�c�̊O�S���e�Ƃ���B�ӎO�p�`�`�e�a����A�`�c�͐��O�p�`�e�a�c�̑Ώ̎� |
�P�U�W
�i�S�O�C�Q�O�C�P�O�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�@�V�O |
���a�b�c�̊O�S�e�A�e�a�b�`�͉~�ɓ��ڂ���B�e�a�V�`�b���瓙�r��`�e�a�b�`�A���`�e�c�߁��b�a�c |
�P�U�X
�i�S�O�C�R�O�C�R�O�C�V�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
�g�s�b�N�X�̖��k�P�W |
�P�V�O
�i�S�O�C�R�O�C�R�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
���a�b�c�̊O�S�e���Ƃ�B���e�a�b�͒��p�S�O�̓ӎO�p�`����A�a�C�`�C�e�͓��꒼����B�`�c�̓^�R�`�e�`�b�c�̑Ώ̎� |
�P�V�P
�i�S�O�C�R�O�C�S�O�C�U�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
���X�Q�ԂƓ��l |
�P�V�Q
�i�S�O�C�R�O�C�V�O�C�V�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
���X�P�ԂƓ��l |
�P�V�R
�i�S�O�C�R�O�C�W�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�U�O |
���T�X�ԂƓ��l |
�P�V�S
�i�S�O�C�R�O�C�W�O�C�U�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
���X�S�ԂƓ��l |
�P�V�T
�i�S�O�C�U�O�C�R�O�C�V�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
���`�a�b���`�b�Ő܂�Ԃ��a���e�A�b�e�Ƃa�`�̌�_�f�Ƃ���B�f�a�b�c�͉~�ɓ��ځB�f�e���f�c���e�c���f�` |
�P�V�U
�i�S�O�C�U�O�C�T�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
���P�R�ԂƓ��l |
�P�V�V
�i�S�O�C�V�O�C�Q�O�C�U�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
�d�c�ԂɁڂ`�e�d���Q�O�ƂȂ�e���Ƃ�B�e�`�a�b�͉~�ɓ��ڂ���B�e�b���b�`�A���c�e�b�̊O�S�f�Ƃ���B���c�e�f�߁��e�`�b |
�P�V�W
�i�S�O�C�V�O�C�R�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
���P�O�X�ԂƓ��l |
�P�V�X
�i�S�O�C�V�O�C�S�O�C�U�O�j
�@�@�@�@�@�@�@�@�@�@�P�O |
���a�b�c�̊O�S�e�B�a���`�b�ɐ��������낵�e�b�Ƃ̌�_�f�Ƃ���B�`�a�b�f�̓^�R�`�ŁA�`�a�f�e���^�R�`�B�`�C�e�C�c�͓��꒼����B |
�P�W�O
�i�S�O�C�V�O�C�T�O�C�T�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
�ڂ`�d�a�̓����Ƃb�a�C�b�e�Ƃ̌�_�f�C�e�Ƃ���B���d�f�b�߁��d�c�b�A�b�`�́��b�f�c�̑Ώ̎��B�f�́��`�d�a�̖T�S |
�P�W�P
�i�T�O�C�Q�O�C�S�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
�b�`���b�a�A�`�̔��Α��ɐ��O�p�`�a�b�e�����B�d�a�e�b�͉~�ɓ��ڂ���B���`�d�e�߁��c�d�e |
�P�W�Q
�i�T�O�C�Q�O�C�V�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
���P�T�W�ԂƓ��l |
�P�W�R
�i�T�O�C�R�O�C�R�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
�`���ɐ��O�p�`�a�b�e�����B�`�b�C�a�c�͂��̑Ώ̎��B�ڂ`�e�a���Q�O�A�ڂc�e�b���T�O�A�e�`�a�c�͉~�ɓ��ڂ���B |
�P�W�S
�i�T�O�C�R�O�C�S�O�C�V�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
���c�a�b�̊O�S�e�B�b�c���c�d���c�e���e�b�A�`�a�d�e�͉~�ɓ��ځB���`�e�c�߁��`�e�b |
�P�W�T
�i�T�O�C�R�O�C�U�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
���P�V�O�ԂƓ��l |
�P�W�U
�i�T�O�C�R�O�C�V�O�C�V�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
���P�R�ԂƓ��l |
�P�W�V
�i�U�O�C�Q�O�C�R�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�@�Q�O |
���P�S�O�ԂƓ��l |
�P�W�R
�i�U�O�C�Q�O�C�T�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�S�O |
���P�Q�P�ԂƓ��l |
�P�W�X
�i�U�O�C�Q�O�C�T�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�@�Q�O |
���a�b�c�̊O�S�e�A�a�c�Ƃe�b�̌�_�f�Ƃ���B�`�a���a�b���a�f�B���`�a�f�Ɓ��e�a�c�͐��O�p�`�ł��̑Ώ̐�������� |
�P�X�O
�i�U�O�C�Q�O�C�V�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�S�O |
���`�a�b���`�b�Ő܂�Ԃ��B�a���e�A���`�a�b�̊O�S�f�Ƃ���B���O�p�`�f�a�b����A���f�`�b�߁��e�c�b�ŁA�`�b���b�c |
�P�X�P
�i�U�O�C�S�O�C�R�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
�g�s�b�N�X�̖��k�Q�O�Ɠ��l |
�P�X�Q
�i�U�O�C�S�O�C�T�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�Q�O |
���a�b�c���a�c�Ő܂�Ԃ��A�b���e�A�c�e�Ƃb�a�̌�_�f�A�e�c�ԂɁڂc�b�g���Q�O�ƂȂ�g�B�`�f�a�e�͉~�ɓ��ځA�`�́��f�g�b�̊O�S |
�P�X�R
�i�V�O�C�P�O�C�S�O�C�P�P�O�j
�@�@�@�@�@�@�@�@�@�@�@�R�O |
�a�c��Ɂڂa�`�e���S�O�̂e�A�c���ɐ��O�p�`�`�e�f�����B�`�a���`�f�B�`�a�b�f�͉~�ɓ��ځB���`�a�e�߁��f�e�b�B�`�e�b�c�͉~�Ɂc |
�P�X�S
�i�V�O�C�P�O�C�T�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�S�O |
�`�̔��Α��ɐ��O�p�`�a�b�e�����B�a�c�́��`�a�e�̑Ώ̎��A�ڂ`�c�a���ڂa�c�e�B���a�c�b�߁��e�c�b |
�P�X�T
�i�V�O�C�P�O�C�T�O�C�P�P�O�j
�@�@�@�@�@�@�@�@�@�@�@�R�O |
�a�d�ԂɁڂ`�e�a���V�O�ƂȂ�e���Ƃ�ƁA�`�e���`�a���a�b���b�c�łQ�p��ӂ���A���`�e�d�߁��c�b�d�B�`�d���d�c |
�P�X�U
�i�V�O�C�P�O�C�U�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�@�S�O |
�`���ɐ��O�p�`�b�c�e�����B�ڂa�e�b���S�O�B���r��`�`�a�b�e���A�`�e���a�b���e�c�A�ڂe�c�`���P�O |
�P�X�U
�i�V�O�C�R�O�C�Q�O�C�P�P�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
�a�c��Ɂڂb�`�e���Q�O�̂e�A�a�b��Ɂڂa�`�f���Q�O�̂f���Ƃ�B�`�a�f�e�̓^�R�`�B�e�́��`�f�b�̓��S�B�`�e�b�c�͉~�ɓ��ڂ���B |
�P�X�W
�i�V�O�C�R�O�C�R�O�C�P�P�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
�`���ɐ��O�p�`�e�a�b�����B�`�b�C�a�c�͂��̑Ώ̎��B�ڂ`�e�a�Ɓڂa�e�b�Ɓڂb�e�c����A�`�C�e�C�c�͓��꒼���� |
�P�X�X
�i�V�O�C�R�O�C�T�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�S�O |
���P�O�X�ԂƓ��l |
�Q�O�O
�i�V�O�C�R�O�C�U�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�S�O |
���a�b�c�̊O�S�e�A�e�a�Ƃ`�b�̌�_�f�B�`�a�b�e�͓��r��`�ł`�b���a�e���e�b���b�c�B���`�b�c�ʼn��� |
�Q�O�P
�i�V�O�C�S�O�C�Q�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
���`�a�b�̊O�S�e�A�`�e���e�b�A���c�e�b���`�e�̏㕔�ɓ\��t���c���f�Ƃ���B���O�p�`�f�e�c����A�f�́��`�c�e�̊O�S |
�Q�O�Q
�i�V�O�C�S�O�C�R�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�@�P�O |
�a�d�ԂɁڂd�`�e���P�O�ƂȂ�e�A�e���`�a�ɐ���FH�����낵�A�����CB�Ƃ̌�_��G�Ƃ���AF�́�AGC�̊O�S�AAFCD�͉~�Ɂc |
�Q�O�R
�i�V�O�C�S�O�C�S�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
���V�Q�ԂƓ��l |
�Q�O�S
�i�V�O�C�S�O�C�T�O�C�W�O�j
�@�@�@�@�@�@�@�@�@�@�R�O |
BD��Ɂ�BFC=�Q�O�ƂȂ�F���Ƃ�AABCF�͉~�ɓ��ځBFD�̏㕔�Ɂ�ACF��\��t���BA��G�Ƃ���BG�́�ADF�̊O�S |
�Q�O�T
�i�W�O�C�Q�O�C�R�O�C�P�P�O�j
�@�@�@�@�@�@�@�@�@�@�@�Q�O |
���P�X�U�ԂƓ��l |
�Q�O�U
�i�W�O�C�Q�O�C�S�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�@�R�O |
���P�X�T�ԂƓ��l |
�Q�O�V
�i�W�O�C�Q�O�C�S�O�C�P�P�O�j
�@�@�@�@�@�@�@�@�@�@�@�Q�O |
���P�X�S�ԂƓ��l |
�Q�O�W
�i�W�O�C�Q�O�C�T�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�@�R�O |
���V�Q�ԂƓ��l |
�Q�O�X
�i�W�O�C�R�O�C�R�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�@�Q�O |
���P�X�W�ԂƓ��l |
�Q�P�O
�i�W�O�C�R�O�C�S�O�C�P�O�O�j
�@�@�@�@�@�@�@�@�@�@�@�Q�O |
���P�O�X�ԂƓ��l |
�Q�P�P
�i�P�O�O�C�P�O�C�R�O�C�P�R�O�j
�@�@�@�@�@�@�@�@�@�@�@�@�Q�O |
BC=CD�AA���ɐ��O�p�`CDF�����BABCF�͉~�ɓ��ڂ��AAF=AC����AACDF�̓^�R�` |
�Q�P�Q
�i�P�O�O�C�P�O�C�S�O�C�P�Q�O�j
�@�@�@�@�@�@�@�@�@�@�@�@�R�O |
BC=CD�A��ABC�̊O�SF�Ƃ���B��AFB�A��CFD����AA,F,D�͓��꒼���� |
�Q�P�R
�i�P�O�O�C�Q�O�C�Q�O�C�P�R�O�j
�@�@�@�@�@�@�@�@�@�@�@�@�P�O |
BD�ԂɁ�BCF=�P�Q�O��F���Ƃ�ƁA�Ώ̐�����A���r��`ABCF�BA�̔��Α��ɐ��O�p�`FCG�����ƕ��s�l�ӌ`ABGF�B |
�Q�P�S
�i�P�O�O�C�Q�O�C�S�O�C�P�P�O�j
�@�@�@�@�@�@�@�@�@�@�@�@�R�O |
��BCD�̊O�SF�����B�l�p�`ABCF�͉~�ɓ��ڂ��AAB=AF�B�l�p�`ABDF�̓^�R�`�B |
�Q�P�T
�i�P�O�O�C�R�O�C�Q�O�C�P�Q�O�j
�@�@�@�@�@�@�@�@�@�@�@�@�P�O |
�g�s�b�N�X�̖��k�Q�O |
�Q�P�U
�i�P�O�O�C�R�O�C�R�O�C�P�P�O�j
�@�@�@�@�@�@�@�@�@�@�@�@�Q�O |
��ABC�̊O�SF�ABD�ԂɁ�DCG=10��G���Ƃ�B��BCG�̊O�S��F�A��FCD�̊O�S��G�ƂȂ�cA,F,D�͓��꒼���� |

 �@
�@