 |
| 問題 11 (20,60,50,30) |
この問題が本来「ラングレーの問題」といわれています。 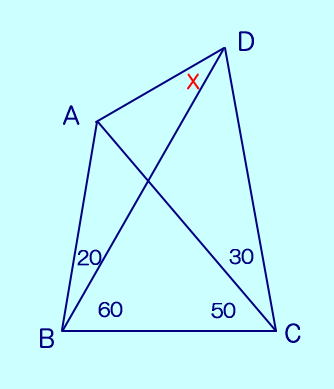 |
↓
↓
↓
[解答]
↓
↓
下図の△ABCは 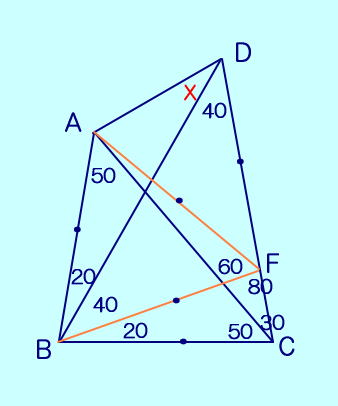 |
| 以前「なぜ、正三角形を作るとうまく解けるんですか?」という質問があったのですが、「正三角形はどこから見ても二等辺三角形だから…」というわけのわからない返事をしてしまいました。今でも、自分としていい返事をすることができません。これを解決するためには星の入ったボールを7つ集めるしかないか…その前にドラゴンレーダーを入手… |
[別の解答] ↓図、正三角形ABFを作ると。 AB=BC=BF から、 点B は△AFCの外心になり BDとFCの交点をGとすると、 △FBGは二等辺三角形より FB=FG=FAから、 点F は△ABGの外心になる。 ∠AGD=∠ABG+∠BAG =20+10=30 ∠AGD=∠ACD が成り立ち 四角形AGCDは円に内接する。 ∠ADB=∠ACG=30 答え 30° 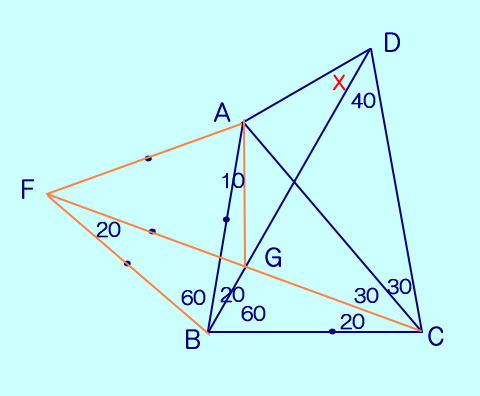 |
|
[類題1] (30,10,120,40) 答え 30° |
| 「ラングレーの問題」とグーグルなどで検索するといろいろ出てきます。上の解答以外にも別の補助線を引いたり、高校で習う「三角比」を用いる証明もあります。上の図で辺BAと辺CDの延長線の交点をPとした頂角20°の二等辺三角形 PABを問題の出発点とするラングレーの問題も多くあります。中でも技術系サラリーマンの交差点の5年考えて解けなかった問題においてはこの問題11番(20,60,50,30)をいろいろな解法の紹介や、解けなかった方の感想があります。 |