| [傍心の角度の関係] |
傍心Dと△ABCの内角の和から 2b+(180−2a)+ (180−2c)=180 より、 a+c=90+b ∠ADC=180−(a+c) =90−b よって ∠ADC=90−∠ABC/2 また、△ABC の外角から ∠ACB=2a−2b,△ABDの外角から ∠ADB=a−b よって ∠ADB=∠ACB/2 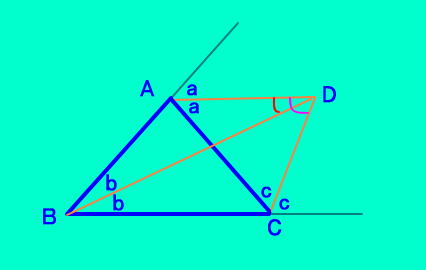 |
| [例題1]問題(30,30,20,80) |
[例題1の解答】 △ABC の∠ABCの内角の 二等分線と、∠ACBの外角の 二等分線の交点Dは △ABCの傍心 よって、 ∠ADB=∠ACB/2 =10° 答え 10° 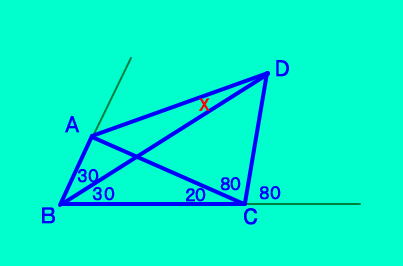 |
| [例題2]問題(40,20,50,80) |
略解 △ACD の∠ACDの外角の 二等分線がBCである。 ∠ABD=∠ACD/2 このとき、点Bは△ACD の傍心になる。 BDは∠ADCの二等分線 ∠ADB=∠BDC=30° 答え 30° 詳しくは下の補足に 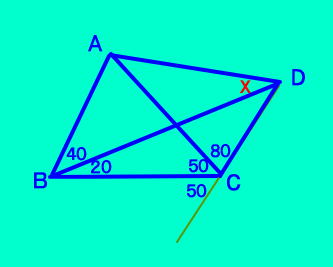 |
[例題2の補足] △点Bより直線DC,AC,DAに 垂線BF,BG,BH をおろす △BFC ≡ △BGC △BGA ≡ △BHA がわかり、このことより △BFD ≡ △BHD ∠ADB=∠BDC BDは∠ADCの二等分線 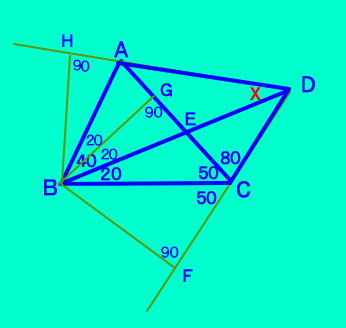 [補足の補足] 傍心で解ける問題は、垂線や外心で 解ける問題も多くあるみたいです。 この問題(40,20,50,80)は、 △ABCの外心O をとると、 四角形AOCDは円に内接する 四角形になって解決します。 ラングレーのページの「問題13」を 参照してみてください。 |
| [定理7]ラングレーB型〜 |
| 四角形ABCDにおいて、 ∠ABD=∠DBC=a ∠BDC=e ∠ADB=f のとき a+e+f=90 を満たすならば、 点Dは△ABCの傍心である。 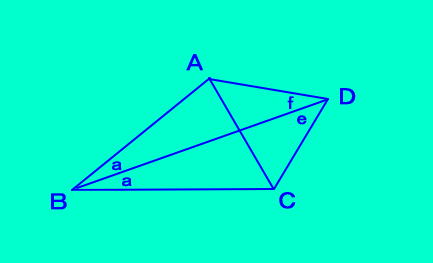 |
| [定理7]のための補題 |
[定理7]のための補題 四角形ABCDにおいて、 ∠ABD=a 、∠BDC=e ∠ADB=f のとき、 a+e+f=90 を満たすならば、 △ABDの外心は 直線DC上にある。 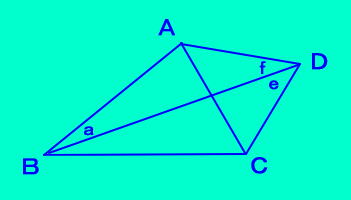 |
上記補題の証明 △ABDの外心を点Oとすると 円周角と中心角の関係から ∠AOB=2f 、∠AOD=2a △OBDは二等辺三角形より、 ∠ODB=(180−(2a+2f))/2 a+f=90ーe から ∠ODB=(180−(180−2e))/2 =e よって、O、C、Dは同一直線上 △ABDの外心Oは 直線DC上にある。 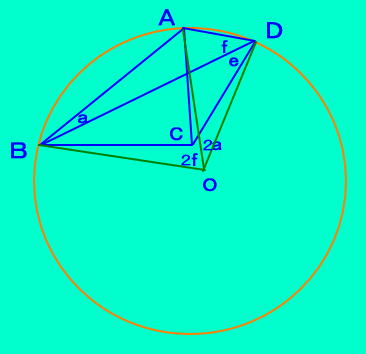 |
[定理7]の証明 BA,BCの延長上にF,Hをとる。 上の補題から a+e+f=90 より△BDCの外心Oは 直線AD上にあり、 その中心角∠COD=2∠CBD =2a ∠ABC=2a から、 4点 O、B,C、Aは同一円周上で ∠BOC=2∠BDC =∠BAC=2e △ABDの内角より、 ∠DAC=180−a−2e−f =180−(a+e+f)−e =180−90−e=90−e ∠FAD=180ー2eー(90−e) =90−e ADは外角FACの二等分線 同様にして CDも外角ACHの二等分線 以上から、点Dは△ABCの傍心 (f<aのとき、外心Oが点Aより 右側の時も同様にいけます。) 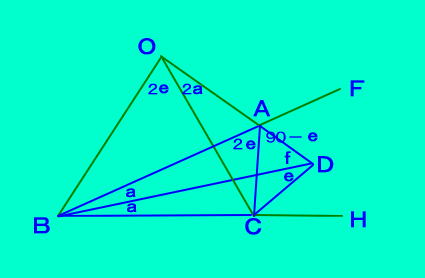 |
| [例題3]問題(20,40,30,30) |
[例題3]の答え 答え 70° 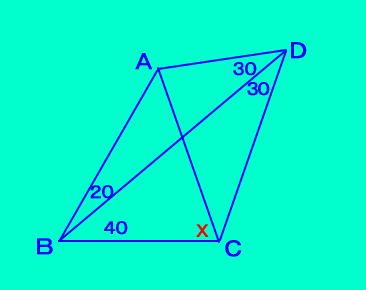 |