外接円、外心について

　それぞれの各辺の垂直二等分線は一点でまじわり、その点Dを中心に円を書くと…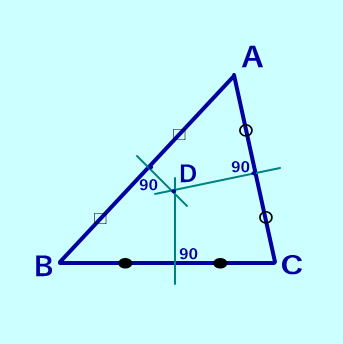

　
  　
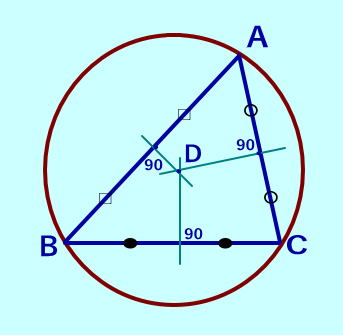Dを中心に三角形の３つの頂点を通る円を書くことができて、この円を「外接円」、その中心Dを「外心」といいます。
　　　　
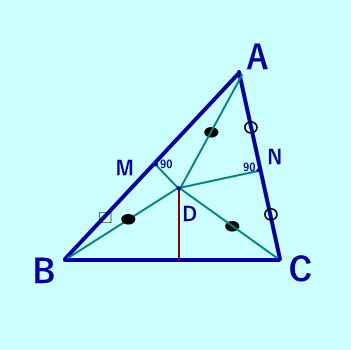
【　三角形の垂直二等分線は　　
　1点で交わることの証明　】
　　
　[証明]

　　　△ＡＢＣにおいて、
　　　辺ＡＢと辺ＡＣの垂直二等分線の
　　　交点をＤとする。△ＡＢＤと△ＡＣＤは
　　　二等辺三角形から、ＤＡ＝ＤＢ＝ＤＣ
　　　よって、
　　　△ＤＢＣも二等辺三角形から、
　　　頂点Ｄは辺ＢＣの垂直二等分線上にある。
　　　
　　　　　　したがって、三角形の三辺の
　　　　　　垂直二等分線は1点で交わる
 


【　三角形の外心の位置　】


鋭角三角形ＡＢＣ
の時↓図、
（どの頂点も９０°より小）
外心Ｏは△ＡＢＣの内部にある。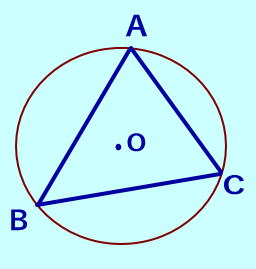


直角三角形ＡＢＣの時↓図

外心Ｏは斜辺の中点にある。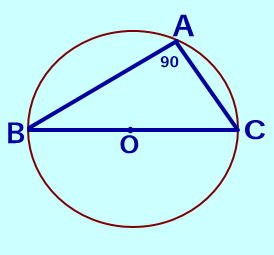

 
  

鈍角三角形ＡＢＣの時↓図
（90°より大の角を持つ）

外心Ｏは鈍角の対応する
辺（下図では辺ＢＣ）の下側にくる。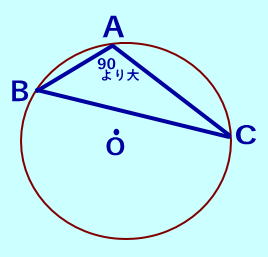


 
【　外心の角度の関係　】


外心の角度の関係　その１　

　△ＡＢＣの外心Ｏをとして、外心Ｏ
　が△ＡＢＣの内部にあるとき、外
　接円の半径から、３つの二等辺
　三角形がある。その底角を図の
　ようにａ，ｂ，ｃ，とすると、
　　
　　２ａ＋２ｂ＋２ｃ＝１８０°
　　２でわって、
　　　　　　ａ＋ｂ＋ｃ＝９０°

　　∠ＢＡＣ＞９０　の鈍角では、
　　　　　　　ｂ＋ｃーａ＝９０°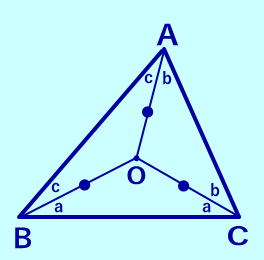


 外心の角度の関係　その２

　∠ＢＤＣ＝Ｘ、∠ＢＡＣ＝Ｙとする。
　　　ｂ＋ｃ＝９０ーａ　より
　　Ｘ＝１８０−２ａ
　　　＝２（９０−ａ）＝２（ｂ＋ｃ）
　　よって、　
　　　　　　　　　Ｘ＝２Ｙ

　　もちろんこれは、
　　円周角と中心角の関係です。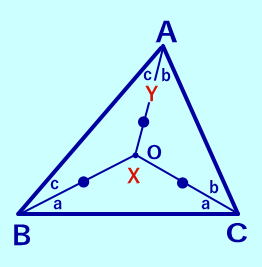

 
外心の基本問題〜
 外心Ｏとして、∠Ｘ を求める
 
 答え Ｘ＝３５°
 △ABCの外心をＯとして、∠Ｘ を求める
 
 答え X=４０

次の【定理１０】は「ラングレーの問題」以外でも
このホームページでは良く用いています。
「定理１０」とことわらないでも使用しています。
【定理１０】

　　↓図　△ＡＢＣについて、∠Ａ＝ａとして、
　０＜ａ＜９０で、点Ｄが、
　辺BCに対してA側にあって、
　∠ＢＤＣ＝２ａ　　を満たし、
　　　　ＢＤ＝ＤＣ　　のとき、
　点Ｄは△ＡＢＣの外心になる。

　∠Ａ＞９０　のときは
　点Ｄは辺ＢＣについて、
　頂点Ａとは反対がわにある。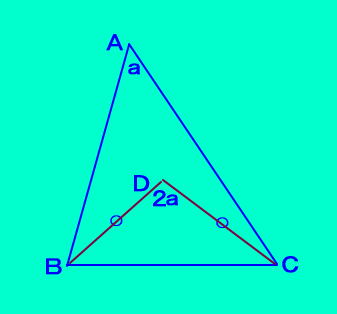


　

 【定理１０の証明】
　
↓図は　０＜ａ＜９０について、
　二等辺三角形ＤＢＣから、
∠ＢＤＣ＝２ａ　なので、
　∠ＤＢＣ＝∠ＤＣＢ＝９０−ａ
　△ＡＢＣの外心をＯとする。
　外心の性質から、ＯＢ＝ＯＣ
　∠ＢＯＣ＝２ａ、よって、
　∠ＯＢＣ＝∠ＯＣＢ＝９０−ａ
　ＢＣが共通していることから、
　△ＤＢＣ≡△ＯＢＣ（2角夾辺）
　よって、点Ｄと点Ｏは一致する。
　点Ｄは外心である。
　
　∠Ａ＞９０　のときは　…略…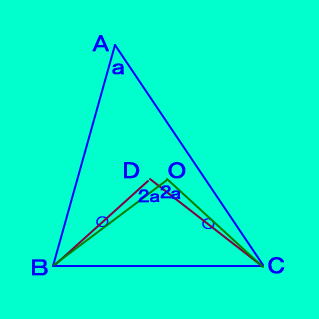

 

この「定理１０」は円周角と中心角の関係から見れば、
明らかかもしれません　

【定理１０】　を用いる例題

　【例題１】

↓図の∠ＤＡＣは？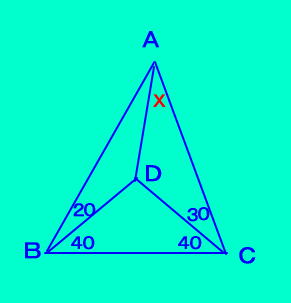



　【解答】
　　∠ＢＡＣ＝５０
　　∠ＢＤＣ＝１００＝２∠ＢＡＣ
　　ＢＤ＝ＤＣより
　　「定理１０」から、点Ｄは
　　△ＡＢＣの外心
　　よって、
　　∠ＤＡＣ＝∠ＤＣＡ＝３０°　

【例題２】

　　↓図の∠ＡＤＢは？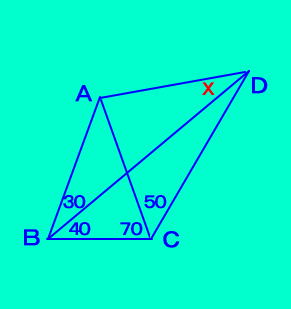



【解答】
　　∠ＢＤＣ＝２０
　　∠ＢＡＣ＝４０＝２∠ＢＤＣ
　　∠ＡＢＣ＝∠ＡＣＢ　より
　　ＡＢ＝ＡＣ
　　「定理１０」から、点Ａは
　　△ＤＢＣの外心
　　よって、
　　ＡＢ＝ＡＤから、
　　∠ＡＤＢ＝∠ＡＢＤ＝３０°
　　 

 【例題３】

　　　　↓図の∠ＡＣＢは？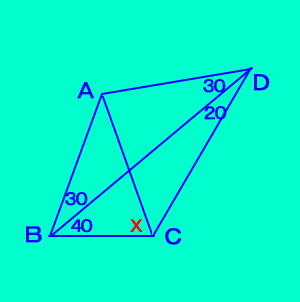



　【解答】
　　∠ＢＣＤ＝１２０、
　　∠ＢＡＤ＝１２０　から、
　　∠ＢＡＤ（優角）＝３６０−１２０
　　　　＝２４０＝２∠ＢＣＤ
　　また、∠ＡＢＤ＝∠ＡＤＢ　より、
　ＡＢ＝ＡＤ　「定理１０」から、点Ａは
　　　△ＤＢＣの外心　よって、
　　　ＡＣ＝ＡＤから、
∠ＡＣＤ＝∠ＡＤＣ＝７０°
　
　優角　…とはその角度の鋭角ではない鈍角のほうです。 
【問題１】

△ＡＢＣはＡＢ≠ＡＣで、
　内部の点Ｄは
　∠ＤＢＣ＝∠ＤＣＢ＝ａ
　∠ＢＡＤ＝ｃ　∠ＡＣＤ＝ｂ
　ａ＋ｂ＋ｃ＝９０°
　このとき、点Ｄは外心である
　　　ことを証明しなさい。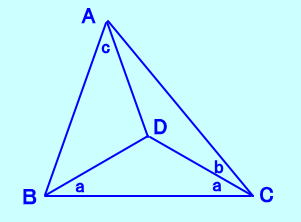