 |
| 補助線の練習その１ 正方形と正三角形 |
下の例題は中学２年の図形の二等辺 三角形のところに出てくる問題です。 ［例題１，２］ それぞれの四角形ＡＢＣＤは正方形で、 △ＰＢＣ、△ＱＡＤは正三角形として、 ∠Ｘ，∠Ｙをそれぞれ求めなさい。  ［例題１の解答］ 正方形ＡＢＣＤより ＡＢ＝ＢＣ 正三角形ＰＢＣより ＢＣ＝ＰＢ よって、ＡＢ＝ＰＢ また、 ∠ＡＢＰ＝∠ＡＢＣ−∠ＰＢＣ ＝９０ ー ６０ ＝ ３０ 二等辺三角形ＡＢＰより∠ＡＰＢ＝７５ △ＰＣＤも同様にして、∠ＤＰＣ＝７５ ∠ＡＰＤ＝３６０−（７５＋７５＋６０）＝１５０ （答え）∠ＡＰＤ＝１５０° ［例題２の解答］ 正方形ＡＢＣＤより ＡＢ＝ＡＤ 正三角形ＱＡＤより ＡＤ＝ＡＱ よって、ＡＢ＝ＡＱ また、 ∠ＱＡＢ＝∠ＤＡＢ＋∠ＤＡＱ ＝９０ ＋ ６０ ＝ １５０ 二等辺三角形ＡＢＱより ∠ＡＱＢ＝１５、また△ＤＣＱも 同様にして、∠ＤＱＣ＝１５ ∠ＢＱＣ＝６０−（１５＋１５）＝３０ （答え）∠ＢＱＣ＝３０° |
| 以上の問題は中学２年生の教科書のワーク あたりにはよくあります。これに対して、↓の 問題は角度の問題の難問かもしれません。 もちろん、中2の教科書や教科書のワーク等に はありません。 最近（2014年）GooglePlayの数学クイズ なん度？ というアプリでファイナルステージの最終問題の 20番についての問い合わせがあったので、 この20番については下↓（アプリの問題とは図が 上下が逆）の【問題１】を参考にしてみて下さい。 もしファイナルステージが終わられている方は その下の[問題２]以降の問題に挑戦してみては？ いちおうの解答も2通りほどは付けています。 |
［問題１］ 正方形ＡＢＣＤの中に ＡＤを底辺とし、∠ＡＰＤ＝１５０ の二等辺三角形ＡＰＤ があるとき∠ＢＰＣは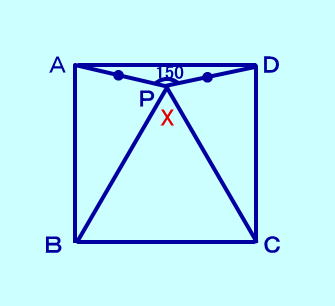？  ［問題１の答え］ コークスター「幾何学再入門」（1970年） にあった問題です。 |
［問題２］ 正方形ＡＢＣＤのＢＣを底辺とし 図のような∠ＢＱＣ＝３０の 二等辺三角形ＢＱＣが あるとき∠ＡＱＤは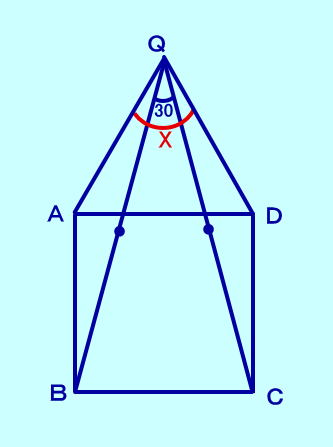？  ［問題２の答え］ |
| 補助線の練習…形をあてはめてみる |
| 下の〈図Ａ〉について このページのはじめの例題１，２をもとにすると、下のような角度の関係があります。この図を以下〈図Ａ〉と呼ぶことにします。このことを知っているということを前提にするとこのあとの問題の補助線は引きやすくなります。ただ、その補助線がベストとは限らないかもしれませんが補助線の練習になると思います。図には入れていませんが、正方形の対角線も書き加えるといいと思います。 |
 |
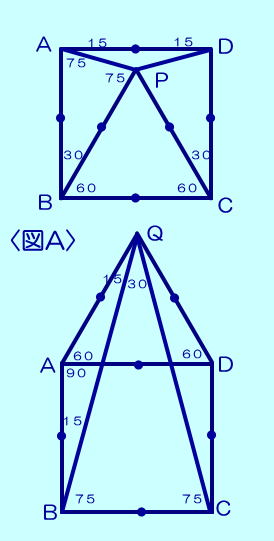［例題3］ ∠Ａを直角とする直角二等辺 三角形ＡＢＣにおいて点Ｄは ∠ＡＢＤ＝３０、ＡＢ＝ＡＣ＝ＢＤ をみたすとき、 ∠ＤＣＢは？  |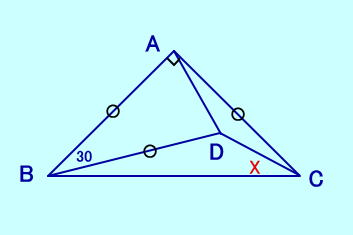
［例題3の答え］ 図のような、正方形ＣＡＢＥ を作る。∠ＤＢＥ＝９０−３０＝６０ △ＤＢＥは正三角形 ＤＥ＝ＢＥ＝ＥＣより △ＤＣＥは頂角３０の 二等辺三角形より ∠ＤＣＢ＝∠ＤＣＥー∠ＢＣＥ ＝７５−４５＝３０  |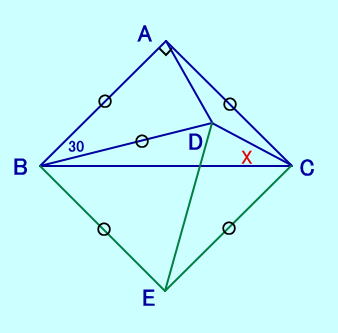
| 次の問題はすべて、上の〈図Ａ〉をもとに 作られています。それでは、やってみましょう！ なかには、〈図Ａ〉の正方形や正三角形を あてはめない方がよいのもあります。 |
［問題３］ ＢＡ＝ＡＤ＝ＤＣ、∠ＢＡＤ＝１５０ ∠ＡＤＣ＝９０、 ∠ＡＢＣは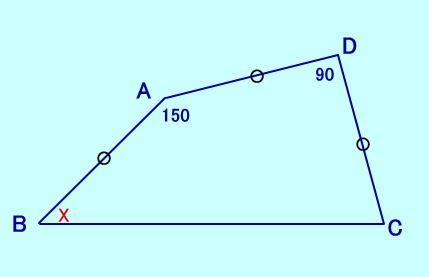？  [問題３の解答] |
［問題４］ （問題３の図と同じ形です） ∠ＢＡＣ＝45、∠ＡＣＢ＝４５ ∠ＤＡＣ＝３０、∠ＡＣＤ＝１０５ ∠ＡＤＢは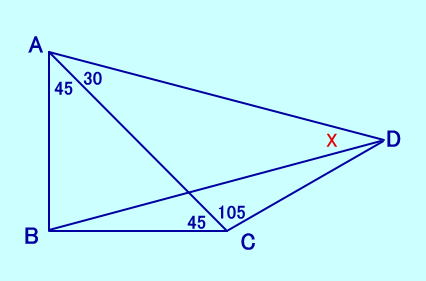？  [問題４の解答] |
［問題５］ ∠ＤＢＣ＝∠ＤＣＡ＝∠ＤＡＣ＝１５ ∠ＤＣＢ＝３０、 ∠ＢＡＤは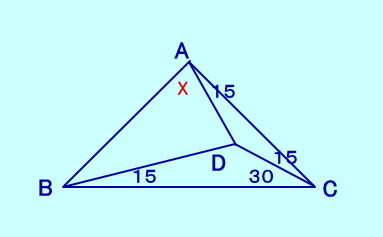？  [問題５の解答] |
［問題６］ ∠ＢＡＣ＝４５、∠ＣＡＤ＝３０ ∠ＢＤＣ＝１５、∠ＡＤＢ＝３０ ∠ＡＣＢは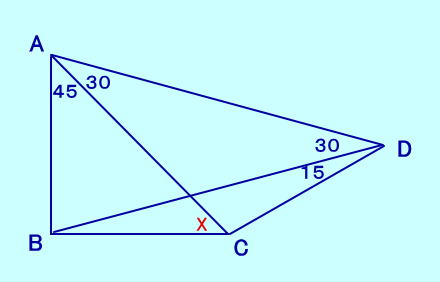？  [問題６の解答] |
［問題７］ ∠ＡＢＤ＝１５、∠ＤＢＣ＝４５ ∠ＡＤＢ＝３０、∠ＢＤＣ＝４５ ∠ＢＡＣは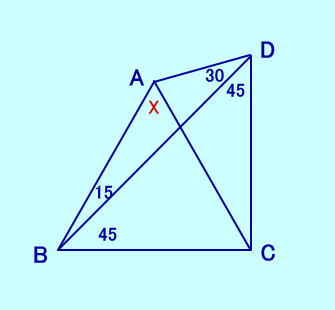？  [問題７の答え] |
［問題8］ ∠ＤAＣ＝15、∠ＤＢＣ＝15 ∠ＤCB＝３０、∠ＤＡＢ＝７５ ∠ABＤは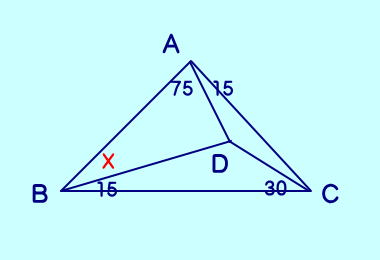？  [問題８の答え] |
［問題９］ ∠ＤＢＣ＝４５、∠ＡＣＢ＝１５ ∠ＡＣＤ＝３０、∠ＡＤＢ＝４５ ∠ＡＢＤは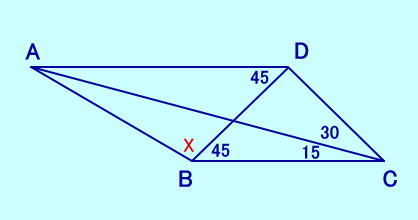？  （この問題は 「算数オリンピックに挑 戦９５〜９９」ブルーバックスにあります） [問題９の答え] |
［問題１０］ ∠BDC＝９０、∠DBC＝４５ ∠ADB＝４５、 CB＝CA を満たすとき、 ∠ACBは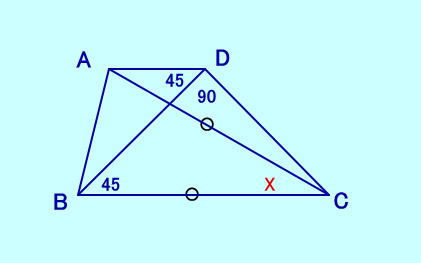？  （清宮先生のモノグラフ「幾何学」 「理系への数学」 によると 、この形の問題は古くからある難問だそうです） [問題１０の答え] |
| ［問題１１］ ∠ＡＢＤ＝３０、∠ＤＢＣ＝４５ ∠ＡＣＢ＝３０、∠ＤＣＡ＝１５ ∠ADBは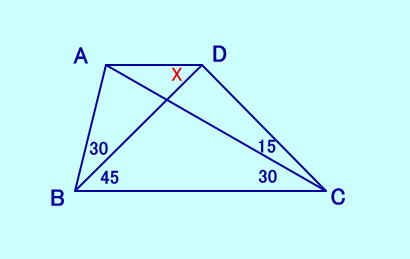？  [問題１１の答え] |
［問題１２］ ∠ＡＢＤ＝３０、∠ＤＢＣ＝４５ ∠ＡＤＢ＝４５、∠ＢＤＣ＝９０ ∠ＡＣＢは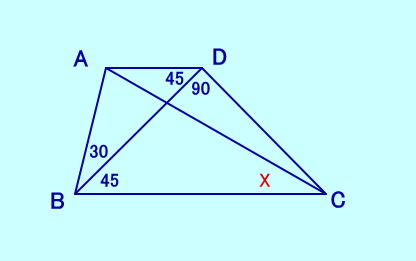？  [問題１２の答え] |
［問題１３］ ∠ＡＢＤ＝３０、∠ＡＣＢ＝３０ ∠ＡＤＢ＝４５、∠ＤＣＡ＝１５ ∠ＢＤＣは？ 分度器と定規とコンパスを持っていたとして、下のような 角度が与えられたとき、図を描け、といったらどのよう に描きますか？（もちろん、Xの値はわからないとして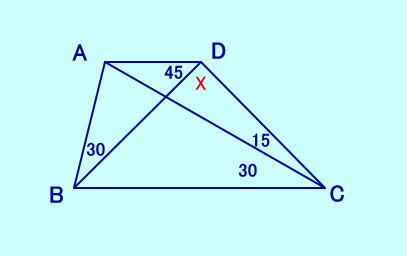）  [問題１３の答え] |
［問題１４］ ∠ＡＢＭ＝３０、∠ＡＣＭ＝１５ ＢＭ＝ＭＣ ∠ＡＭＢは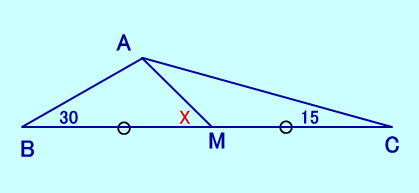？  ［問題１４の答え］ |
［問題１５］ ∠ＣＡＭ＝３０、∠ＡＣＭ＝１５ ＢＭ＝ＭＣ、 ∠ＡＢＭは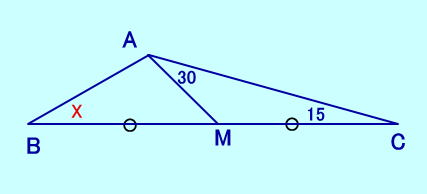？  ［問題１５の答え］ この問題を２つあわせた 平行四辺形として 「数学パズルランド （ブルーバックス）」にあります。 |
［問題１６］ ∠ＡＭＢ＝４５、∠Ｂ＝２∠Ｃ ＢＭ＝ＭＣ、 ∠Ｃは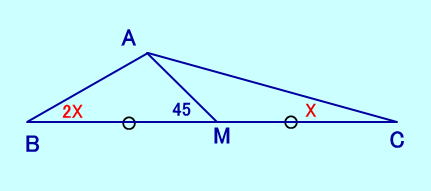？  ［問題１６の答え］ 「エレガントな問題をつくる」にあります。 |
［問題１７］ ∠ＡＭＢ＝４５、 ∠Ｂ＝ＭＡＣ ＢＭ＝ＭＣ、 ∠Ｂは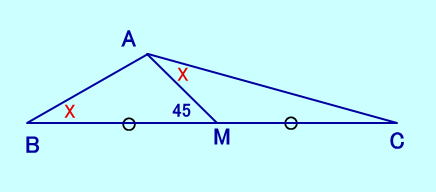？  ［問題１７の答え］ |
［問題１８］ ∠ＭＡＣ＝２∠Ｃ、 ∠Ｂ＝３０ ＢＭ＝ＭＣ、 ∠Ｃは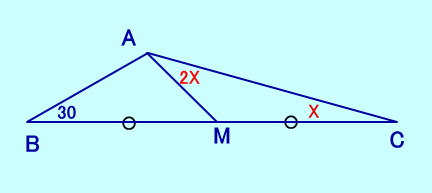？  ［問題１８の答え］ |
［問題１９］ ∠ＭＡＣ＝２∠Ｃ、 ∠ＡBM＝２∠Ｂ ＢＭ＝ＭＣ、 ∠Ｃは？  |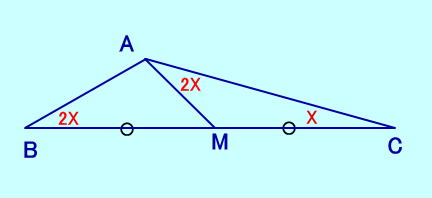
［問題２０］ ∠Ｂ＝３０、∠Ｃ＝１５ ∠ＡMB＝４５ のとき、 ＢＭ＝ＭＣを証明しなさい。  |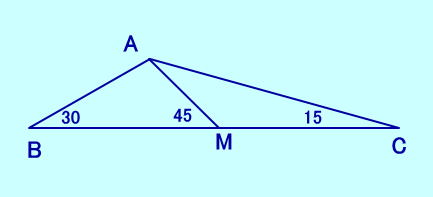
［問題２１］ ∠ＡＢＭ＝１０５、∠ＡＣＭ＝３０ ＢＭ＝ＭＣ、 ∠ＡＭＢは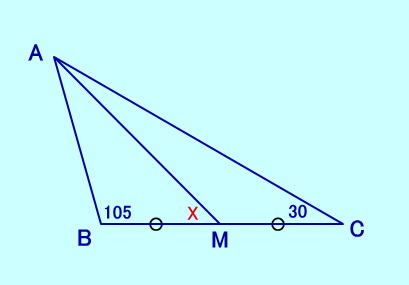？  ［問題２１の答え］ （問題１４）と（問題２１）の２つ の図形を合わせた四角形は円に内接 する四角形にもなっている。 |
［問題２２］ ∠ＢＡＭ＝２∠ＣＡＭ、∠ＡＣＢ＝３０ ＢＭ＝ＭＣ、 ∠ＣＡＭは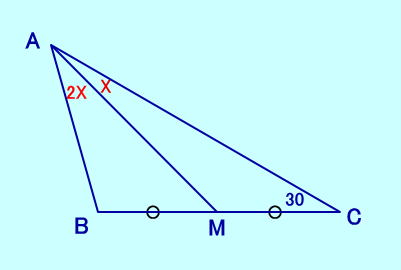？  答えは Ｘ＝１５ それと ３０ |