|
| BASIC + α |
| このページは公立中学校でに習う内 容を基本とし、それとプラスアルファの 内容でこの「スウガクとくガウス」は事 たりるかな~いうわけで、チュートリ アルみたいなもんです。 |
【対頂角】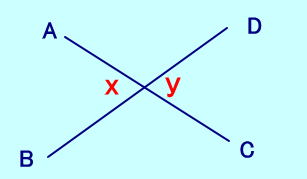 ∠x = ∠y |
【同位角】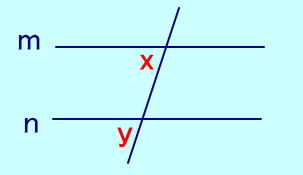 直線m〃直線n ⇔∠x = ∠y |
【錯角】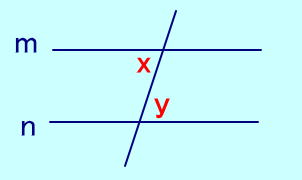 直線m〃直線n ⇔ ∠x = ∠y |
【補角】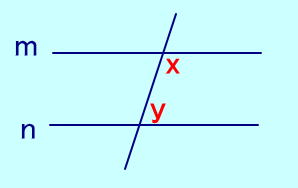 直線m〃直線n ⇔ ∠x+∠y=180° |
【三角形の外角】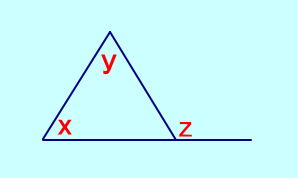 ∠x + ∠y=∠Z |
| 【三角形の合同に関する定理】 |
| ① 3組の辺がそれぞれ等しい。 (3辺相等) ② 2組の辺とその間の角 がそれぞれ等しい。 (2辺夾角相等) ③ 1組の辺とその両端の角 がそれぞれ等しい。 (2角夾辺相等) 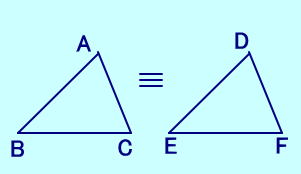 ④ 2組の辺と1対角が等しいとき、 △ABCと△DEFにおいて、 AB=DE、AC=DF、 ∠B=∠E ならば ∠C=∠F または∠C+∠F=180 が成り立つ 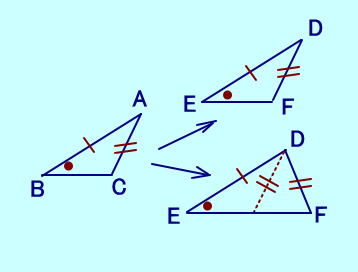 |
| 【直角三角形の定理】 |
| 【合同の定理】 ① 斜辺と1つの鋭角がそれぞれ等しい。 ② 斜辺と他の1辺がそれぞれ等しい。 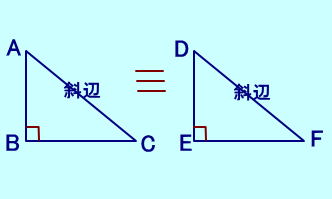 |
| 【定理】 ① 直角三角形ABCの斜辺ACの 中点Mをとると AM=BM=CM がなりたつ。 ② △ABCの辺ACの中点Mをとり AM=BM=CM がなりたつと ∠ABC=90°である。 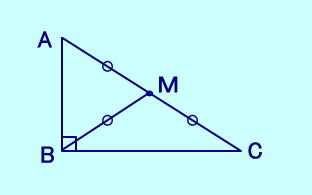 |
| 【二等辺三角形に関するする定義や定理】 |
| 【定義】 二等辺三角形とは二辺が等しい三角形 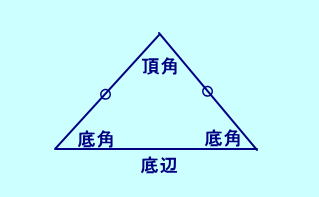 |
| 【定理】 AB=AC ⇔ ∠B=∠C 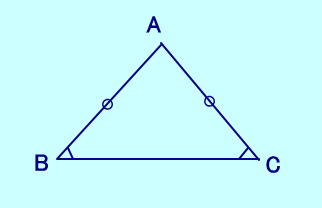 |
| 【定理】 二等辺三角形において、 頂角の二等分線は 底辺の垂直二等分線になる。 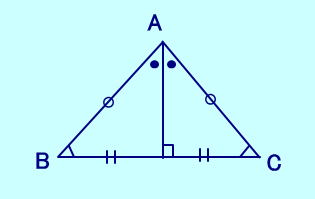 |
| 【 二等辺三角形に関する問題は基本問題ですが問題6は難問です 】 |
| 問題1 鋭角△ABCの頂点B、Cからそれぞれ辺AC、ABに垂線BM,CNをおろしBM=CN ならば、AB=ACを証明しなさい。 |
| 問題2 鋭角△ABCの頂点B、Cからそれぞれ辺AC、ABに垂線BM,CNをおろしMN〃BC ならば、AB=ACを証明しなさい。 |
| 問題3 △ABCの∠B、∠Cの角の二等分線とAC、ABの交点をそれぞれ、D,Eとする。ED〃BCならば、AB=ACを証明しなさい。 |
| 問題4 △ABCのAB、ACの中点をそれぞれM,NとするBN=CM ならば、AB=ACを証明しなさい。 |
| 問題5 △ABCの∠Aの角の二等分線とBCの交点をMとすると、BM=CMならば、AB=ACを証明しなさい。 |
| 問題6 「シュタイナー・レームスの定理」と呼ばれる問題~ △ABCの∠B、∠Cの角の二等分線と AC、ABの交点をそれぞれ、D,Eとする。 BD=CEならば、AB=ACを証明しなさい。 問題6の解答 |
| 問題7 すべての三角形が2等辺三角形であることの証明 ~なにがいけないかを指摘してください(↑クリック) |
| 【平行四辺形に関する定理】 |
| ① 2組の対辺がそれぞれ平行。(定義) ② 2組の対辺がそれぞれ等しい。 ③ 2組の対角がそれぞれ等しい。 ④ 1組の対辺が平行で等しい。 ⑤ 対角線がそれぞれの中点で交わる。 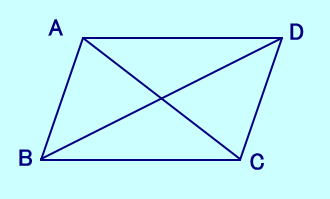 |
| 【上の⑤について】 最近の中二の教科書では⑤では「それぞれ~」という表現だがそれ以前の教科書では「対角線がおのおのの中点で交わる。」という表現が多かったように思われる。「おのおの」は死語になりつつあるのかナー。昔は「オノオノガタ→長谷川一夫→桜井長一郎or林家木久蔵」という流れで「おのおの」は生きていたんだが、「それぞれ」より、いっそのこと管理人は使いたくない表現というより嫌いな表現の「ぜんぜん~肯定表現」でいくと、「対角線がぜんぜん中点で交わる。」のほうが、今風で軽薄的でなかなかよろしい。 「オノオノガタ→長谷川一夫→桜井長一郎or林家木久蔵」の意味がわからない方はそれぞれ検索を!しかしそんな古いギャグは若い人はわかりまへんで…そういうオレって…  |
| 【等脚台形の定義】 |
| 等脚台形とは AD〃BC である台形ABCDにおいて、 ∠B=∠C (または∠A=∠D) を満たすとき等脚台形という。 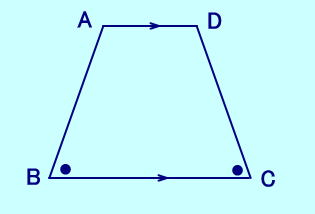 |
| 【等脚台形に関する問題】 |
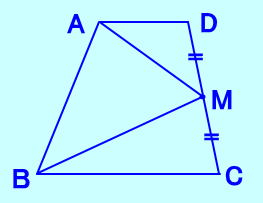
問題8 AD〃BC 、∠B=∠C である等脚台形において AB=DCを証明しなさい。 |
問題9 AD〃BC 、∠B=∠C である等脚台形において 対角線AC=対角線DB を証明しなさい。 |
問題10 平行な2直線と1つの円が4点で 交わるとき、この4点を結ぶ 四角形は等脚台形であること を証明しなさい。 |
問題11 四角形ABCDにおいて AB=CD、∠B=∠C ならば この四角形ABCDは等脚台形で あることを証明しなさい。 |
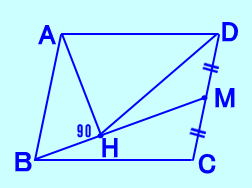
問題12 AD〃BC の台形において 対角線AC=対角線DB ならば この台形は等脚台形である ことを証明しなさい。 |
問題13 AD〃BC の等脚台形(∠B=∠C、 AD<BC) において、 この等脚台形が円に内接することを 証明しなさい。 |
| 問題14 (高校生向き) △ABCにおいて、AB=5、BC=2√3、 CA=4+√3として、次の値を求めよ。 (1) cosAを求めよ。 (2) △ABCの面積 (3) △ABCの外接円Oの半径 Bを通り、CAに平行な直線と円Oとの交点 のうち、Bと異なる方をDとする。 (4) CDの長さ (5) BDの長さ (6) 台形ADBCの面積 ( 答え 12 ) 2003年のセンター試験です。センター試験には図はありませんでしたが、(6)がうまくできなかった受験生は問題の図をある程度はきれいに書くことが必要かもしれません。むしろ、「問題10」は知っとけということカナー |
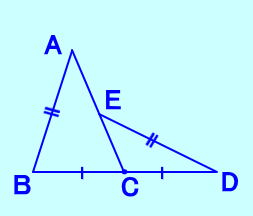
| 【中点連結定理】 |
| △ABCの辺AB,ACの中点を それぞれM,Nとすると、 MN〃BC、MN=BC/2 が成り立つ。 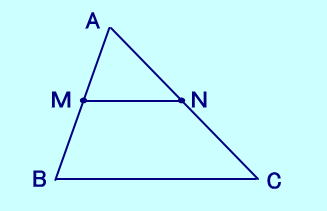 現在、中点連結定理は中3でやっていま すが以前のように中2でやっていたほ うが比の処理も含めて、問題演習に 時間を費やせるように思います。 |
| 【円に関すること】 |
1つの弧に対する円周角は、 その弧に対する中心角の半分 下の図では、 ∠BAC=∠BOC/2 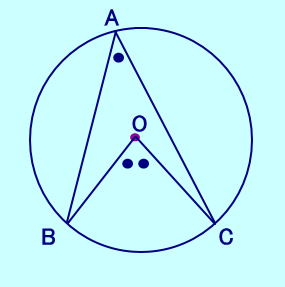 |
1つの弧に対する円周角は等しい。 下の図では、弧BCに対して、 ∠BAC=∠BDC 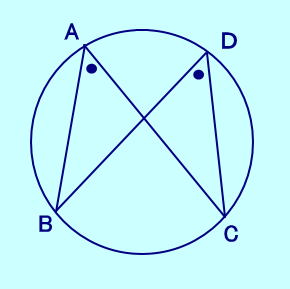 |
円に内接する四角形では、 対角の和は180°です。 下の図では ∠BAD+∠BCD=180° 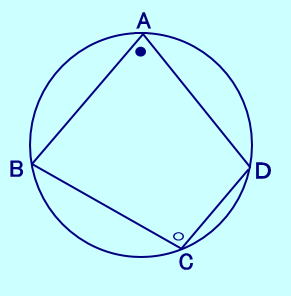 |
円に内接する四角形では 1つの内角は その対角の外角に等しい。 下の図では ∠BAD=∠DCE 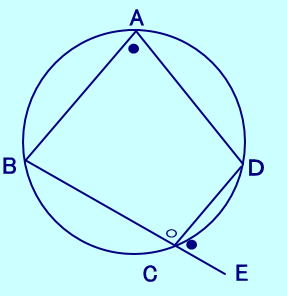 |
| 【4つの点が1つの円周上にあるための条件】 共円条件とも言います。 |
下の図のように線分ABの同じ側に 2点P,Qはあって、 ∠APB=∠AQB が成り立つと 4点A,B,P,Qは1つの円周上にある。 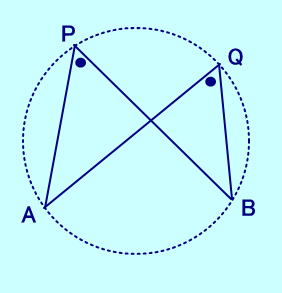 |
下の図のように線分ABの両側に 2点P,Qはあって、 ∠APB+∠AQB=180° が成り立つと 4点A,B,P,Qは1つの円周上にある。 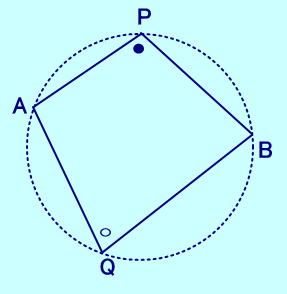 |
接弦定理をやってたころのほうが、円周角
の処理能力が当時の生徒が上だったりして…