垂心について

三角形の３つの頂点から各対辺に垂線を引くと１点で交わる。これを垂心といいます。「垂心」自身は高校で習います。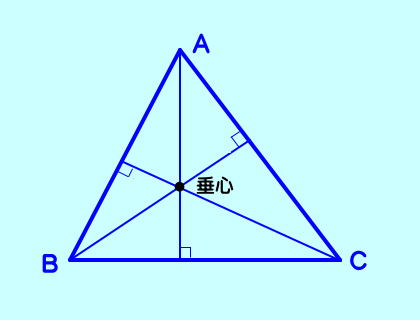

垂心が一点で交わる証明

下の証明のように、２つの頂点から垂線を引き、その交点 と三角形の３っ目の交点を結ぶ直線が三角形の辺に垂直 であればよい…これを、４つの点が同一円周上であること を用いて証明します。垂心が１点で交わる証明は高校で習 うベクトルを使う方法もあります.

{証明｝ 鋭角三角形ABCの頂点B、Cから各辺に 垂線BQ,CPを引き、その交点をHとする。 ∠QRC＝αとして、△QRCにおいて 　∠QCR　＋　α　＝９０° 　∠BPC＝∠BQC　より 　P,B,C,Qは同一円周上にあるから 　∠QPC＝∠QBC＝α 　　　∠APC＋∠AQB＝１８０°より 　A,P,R,Qは同一円周上にあるから 　　　∠QPC＝QAH＝α 　△ARCにおいて 　　∠QCR　＋　α　＝９０°から 　　∠ARC＝９０ 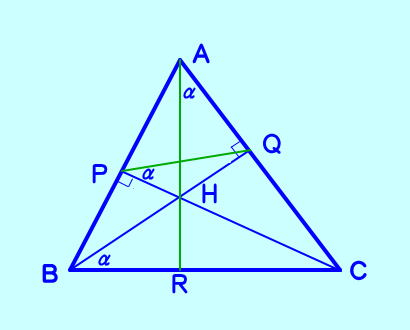　　　　 上の証明では 　　∠QBR=∠QPH＝∠QAH　の利用でした。 それ以外にも 　　∠PBC＝∠AQP＝∠AHP＝∠CHR 　　もアリか

鈍角三角形ABCのとき 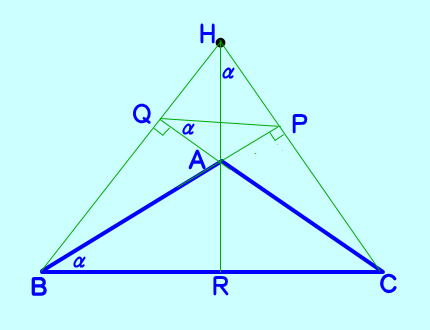　 　Hが垂心となりますが、証明の中身は同様 　直角三角形ABCのときは直角の頂点が垂心

以上のことから、 次のような角度の問題が考えられます

問題

【　問題 １　】 　下の図のXの角度を求めなさい。 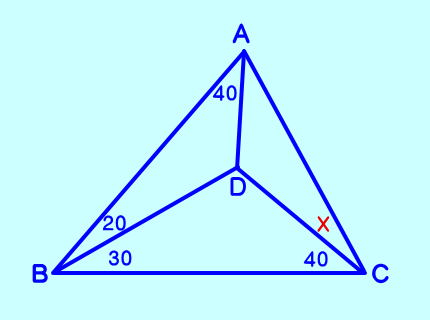　　　　　 　　　AD⊥BC、CD⊥AB,がわかるので点Dは… 　　　　　　　　　　　　　　　　　　　　答え　X＝２０°

【 問題　２ 】 　下の図のXの角度を求めなさい 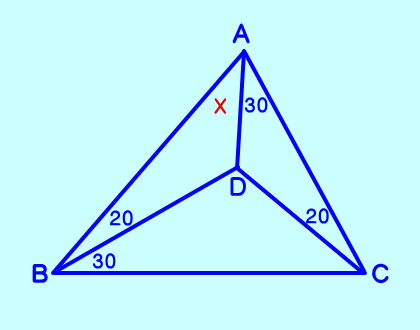　　　　 　　　　前問と同じ図なので、答えは X＝４０ですが、前問と同様というわけでありませんが〜ウルサイ問題でもない