 |
| 擇摍曈嶰妏宍丂偺擄栤 |
| 僔儏僞僀僫乕丒儗乕儉僗偺掕棟 |
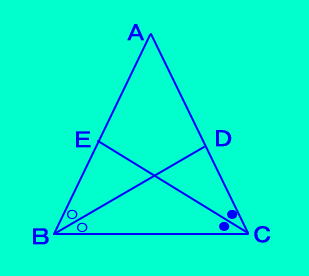
| 丂丂仮俙俛俠偺佢俛丄佢俠偺 丂妏偺擇摍暘慄偲俙俠丄俙俛偺岎揰傪 丂偦傟偧傟丄俢丆俤偲偡傞丅 丂俛俢亖俠俤側傜偽丄 丂丂丂俙俛亖俙俠傪徹柧偟側偝偄丅 |
 |
| 乮Steiner-Lehmus theorem) 忋偺栤戣偼僔儏僞僀僫乕丒儗乕儉僗偺掕棟偲屇偽傟傞 栤戣偱偡丅儕儞僨儞偑偙偺栤戣傪偼偠傔偰傒偨偺偼 孖揷柅愭惗挊乽戝妛傊偺悢妛丂栤戣偼偳偆嶌傜傟傞 偺偐乿乮搶嫗弌斉乯偐傜偱偟偨丅 壓婰偺徹柧伀偼偦偙偵嵹偭偰偄偨傕偺偱偡丅丂 |
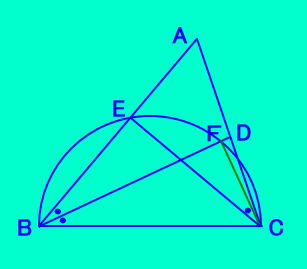
| 亂徹柧亃 丂仮俙俛俠偵偍偄偰丄 丂佢俛亙佢俠丂側傜偽EC亙BD傪徹柧偡傞丅 丂佢俛亙佢俠丂偲偡傞偲 丂佢俛乛俀亙佢俤俠俙 丂恾偺傛偆偵俛俢忋偺佢俢俠俤偺撪晹偵 丂佢俛乛俀亖佢俤俠俥偲側傞揰俥傪偲傞偲丄 丂係揰E,B,C,F偼摨堦墌廃忋偵偁傝 丂丂佢BCF=乮佢B+佢C乯乛俀亙俋侽亱 丂丂佢CBE亙佢BCF亙俋侽亱 丂塻妏偺墌廃妏偱偁傟偽丄墌廃妏偑 丂彫偝偗傟偽丄偦傟偵懳偡傞 丂丂尫偺挿偝傕彫偝偔側傞偺偱丄 丂丂EC亙BF丂傛偭偰丄EC亙BD丂丂乧丂嘆 丂佢俛亜佢俠丂偲偡傞偲丄摨條偵 丂丂丂丂EC亜BD偑惉傝棫偪丂丂丂丂乧丂嘇 丂佢俛亖佢俠丂偲偡傞偲丄柧傜偐偵 丂丂丂擇摍曈嶰妏宍ABC偐傜丄 丂丂丂丂丂丂丂丂丂丂丂丂丂丂EC=BD丂丂乧丂嘊 丂丂嘆丄嘇丄嘊偐傜丄揮姺朄偵傛傝嘊偺媡偺 丂丂EC亖BD側傜偽丄佢俛亖佢俠偑惉棫 |
 |
| 丂亂揮姺朄亃 丂丂丂丂柦戣丂A1仺A2丄B1仺B2丄C1仺C2 丂丂丂乧偑惉傝棫偪壖掕偺A1,B1,C1乧偑 丂丂丂偡傋偰偺応崌傪偮偔偟偰偄偰 丂丂丂寢榑偺A2,B2,C2乧偼偳偺2偮傕 丂丂丂椉棫偡傞偙偲偼側偄丅丂偙偺偲偒丄 丂丂丂媡偺柦戣A2仺A1丄B2仺B1,C2仺C1 丂丂丂乧偼偡傋偰惉傝棫偮丅 |
| 丂僔儏僞僀僫乕丒儗乕儉僗偺掕棟傪 捈愙偟傛偆偲偡傞偲丄壓伀偺曗戣傪徹柧偟偰丄 妏偺擇摍暘斾傗丄摍幃偺娭學偱 僈儞僈儞傗偭偰偄偗偽傛偄丅 乮忋偺恾偱丄EC亖BD傪丄 丂丂丂丂EC丱俀亖BD丱俀偲偟偰巊偆乧乯 乣偲傑偁丄夝愅揑偵夝偔傢偗偱偡偑乧丂 丂徹柧棯 乮仾偙偆偄偆偺傪偆偪偺揷幧偱偼丄 乽傂傘乕側偟乿偲偄偄傑偡偑乧乯 |
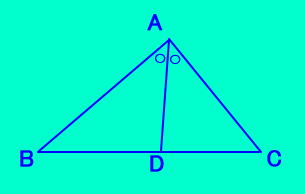
| 亂曗戣亃 丂伀偺仮ABC偺慄暘AD偼佢A偺擇摍暘慄 丂丂偺偲偒丄 丂丂AD丱俀亖AB亊AC乕BD亊DC 丂丂丂丂丂丂丂丂偑惉傝棫偮 丂 丂偙偺徹柧偼 丂丂偦偺侾丂梋尫掕棟傪梡偄傞丅 丂丂偦偺俀丂仮ABC偺奜愙墌傪彂偒AD傪墑挿偟丄 丂丂丂丂丂丂丂墌偵撪愙偡傞巐妏宍偱峫偊傞丅 |
 |
| 丂丂忋偺曗戣偺寢壥偼抦偭偰偍偔偲崅峑惗偺柾帋偁偨傝偱侾偮偺僣乕儖側傞偲巚偄傑偡丅崅峑偱偼丄佢BAC偑桳柤妏偱丄柺愊傪梡偄偰丄AD偺挿偝傪抦傞偙偲偑懡偄偺偱偡偑丄AD偺抣偑僗僩儗乕僩偵弌偰偒傑偡丅AD傪乽僠僃僶慄乿偲偄偆昞尰傕偁傝傑偡丅偙偺懕偒傗暿夝傪抦傝偨偄曽偼伀偺僒僀僩傪朘栤偟偰偔偩偝偄丅 |
| 亂巹揑悢妛弇亃俽丏俫's Homepage for mathematics 丂亜乽巹偺旛朰榐乿 丂亜婔壗妛暘栰亜乽Steiner-Lehmus偺掕棟乿 |
| 丂悢妛偺晹壆亜乽恾宍栤戣僔儕乕僘乿 丂亜亀擇摍曈嶰妏宍丠亁偵偁傝傑偡丅 |
| 丂 悈偺棳傟亜乽棳傟惎乿 丂亜No.177乮嵍僼儗乕儉偺夁嫀栤乯偵偁傝傑偡丅 |
| 忋婰偺孖揷柅愭惗挊乽戝妛傊偺悢妛丂栤戣偼偳偆嶌傜傟傞偺偐乿掕壙1800墌乮搶嫗弌斉乯偼2008擭11寧偵儎僼僆僋偱偺棊嶥嬥妟偑13100墌偱偟偨丅傾儅僝儞偱偺拞屆杮偑2枩墌戜妛廗嶲峫彂側偺偵僪乕僔僥丠偁偲嶳杮嬮堦榊愭惗偺儓儓儓僊儔僀僽儔儕乕偺怟傕儈儑乕僯崅悪丅廐嶳恗愭惗偺弜戜暥屔偺怟傕崅悪丅娗棟恖傕偦傟偧傟偺怟偼壗嶜偐偼帩偭偰偄傑偡偑丄偦傝傖乕偆傟偟偄偗偳偳偆偐偟偰偄傞丅儌僲僌儔僼傒偨偄偵暅崗杮偑偱偰偒偰丄抣抜偑壓偑偭偨傜偄偄偺偵乧倰倧倳倓倎倝巵乮嶲峫彂攷暔娰偺娰挿偝傫仺儕儞僋偺儁乕僕乯偺忣曬偐傜妛廗嶲峫彂愱栧偺屆杮壆丂傪嫵偊偰偄偨偩偒傑偟偨丅 丂丂丂丂丂丂丂丂丂http://www.bookbank.jp/gakusan/post_2.html 丂丂丂丂丂丂丂 |