「補助線の練習その２」 正五角形と正三角形で

［例題１］ 　　　　下の四角形ＡＢＣＤにおいて、 　　　　∠ＡＢＤ＝１２°∠ＤＢＣ＝３６° 　　　　∠ＡＣＢ＝６６°∠ＡＣＤ＝４２° 　　　　∠ＡＤＢを求めなさい。    他の角度を調べると、ＡＢ＝ＢＣ＝ＣＤ、∠ＢＣＤ＝１０８°等から、正５角形の中の１部分と推理して、答えは「天下り談合方式」で書いています。要するに、問題の図は五角形のどかに一致するんだけど〜を出発点で、正三角形を探してみる…

［例題１の答え］ 　　　　 正三角形ＡＢＥを作る。 　　ＤＣ＝ＢＣ＝ＢＡ＝ＡＥ＝ＢＥ 　　∠ＥＢＣ＝∠ＢＣＤ＝１０８ 　　∠ＢＥＣ＝∠ＢＤＣ＝３６、から 　　4点ＥＢＣＤは円に内接する。 　、∠ＥＤＢ＝∠ＥＣＢ＝３６ 　　△ＥＤＢは頂角３６の二等辺三角形で 正三角形ＡＢＥからＡＤはその 対称軸から。∠ＡＤＢ＝３６÷２ 　　　　　　　＝１８　 答え　Ｘ＝１８°

　それぞれの問題は形は違いますが正五角形のどこにある？
〜という問題です。角度に特徴があって、登場する角度は
６の倍数で、６°や７２°などよく出てくる角度があります。

［問題１］  　　上の四角形ＡＢＣＤにおいて、 　　∠ＡＣＢ＝９６、∠ＡＣＤ＝７２ 　　∠ＢＤＣ＝６、∠ＡＤＢ＝６６ 　　のとき、∠ＢＡＣを求めなさい。 正五角形に頂角１６８の二等辺三角形を作るには…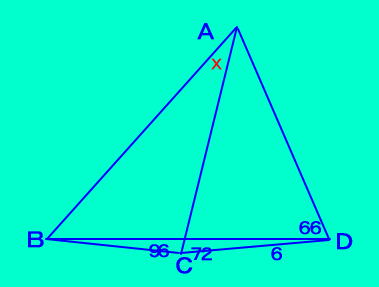

　

［問題２］  四角形ＡＢＣＤにおいて 　∠ＡＢＤ＝３０、∠ＤＢＣ＝６ 　∠ＡＣＢ＝７２、∠ＡＣＤ＝９６ 　のとき∠ＡＤＢを求めなさい。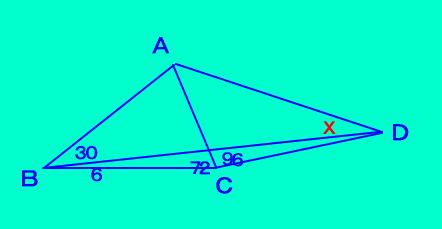

［問題３］ △ＡＢＣとその内部の点Ｄは 　　∠ＡＢＤ＝６、∠ＤＢＣ＝６６ 　　∠ＤＣＢ＝４８、∠ＡＣＤ＝２４ 　　を満たすとき、 　　∠ＤＡＣを求めなさい。 「問題１」と「問題３」は第４回広中杯と条件は 　　　　違いますが、同じ問題。第４回広中杯はここに 　　　　この広中杯の問題も含めて、このような問題を 　　　　イキナリ見て、正五角形が思いつくかどうか、 　　　　　ウ　〜　ン　というところ。正五角形がからむと 角度は６の倍数が多くなりますが。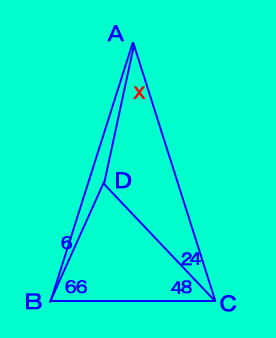

［問題４］  四角形ＡＢＣＤにおいて、 　　∠ＢＣＡ＝３０、∠ＡＣＤ＝６６ 　　∠ＢＤＣ＝１２、∠ＡＤＢ＝５４ 　　を満たすとき、　 　　∠ＢＡＣを求めなさい。 　　あのとがった角度は６°だろう〜 　　それで、正解！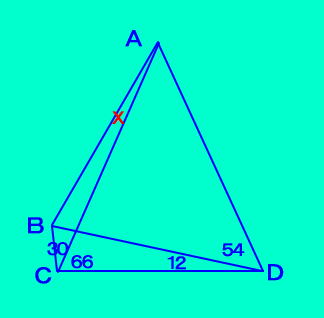

［問題５］ △ＡＢＣにおいて、点Ｄは 　　　∠ＡＢＤ＝１８、∠ＤＢＣ＝３６ 　　　∠ＤＣＢ＝３６、∠ＡＣＤ＝６ 　　　を満たすとき。 　　　∠ＤＡＢを求めなさい。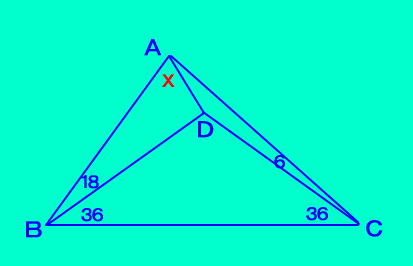

［問題６］ 四角形ＡＢＣＤにおいて、 　　∠ＤＢＣ＝１２、∠ＢＤＣ＝１８　∠ＡＤＢ＝２４ 　　ＡＤ＝ＢＣ　　を満たすとき、∠ＡＢＤを求めなさい 以前、日テレで「世界ジュニア頭脳９３」という番組があ 　　って、ここに出てきた問題（少し条件を変えています） 　　外国の子供がある問題が解けなくて、涙をながしてい 　　たのを覚えています。この［問題６」は 　　「問題３」と同じ雰囲気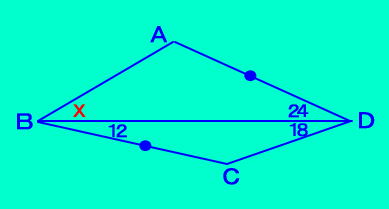