ラングレーＢ型の問題の解答

定理６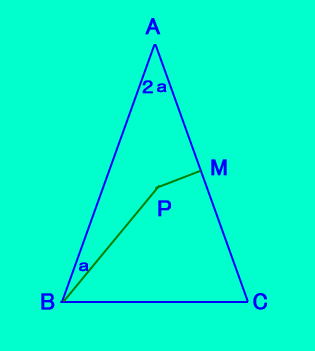 △ＡＢＣは正三角形でない、 AB＝ACの二等辺三角形で、 その内部の点Pが、 ACの垂直二等分線上にある 　すなわち、 　AM＝MC、AC⊥PM かつ、∠ABP＝頂角BACの 半分を満たすならば、APは 頂角BACの二等分線上にある。

証明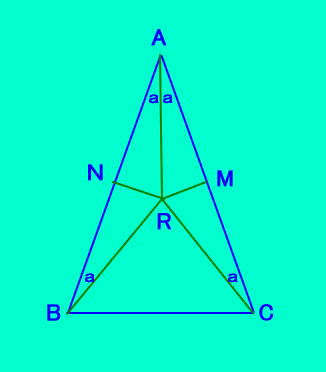 頂角BAC＝２ａ　、ACとABの 中点をMとNとし、ACとABの垂 直二等分線の交点をRとする。 その対称性により、△RABは 底角ａの二等辺三角形よって、 点Rと点Pは一致するので、 AR（P）は頂角の二等分線上にある。

［問題２０　の解答］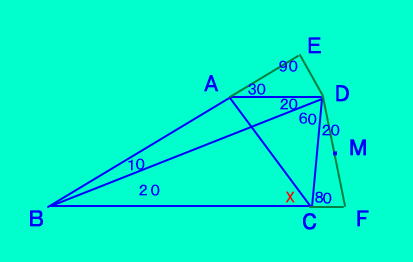

点ＤよりＢＣの延長上に　∠ＣＤＦ＝２０　 　　となるＦをとると　△ＣＤＦは頂角２０の 　二等辺三角形で、ＤＦの中点をＭとし、 　また、ＤよりＢＡの延長上に 　垂線をおろしＥとする。 　△ＢＦＤは頂角２０の二等辺三角形で、 　ＢＭはその対称軸になる。 　２角夾辺から、△ＥＢＤ≡△ＭＢＤ　よって 　ＥＤ＝ＤＭ　ここで　△ＥＡＤは６０°３０°の 　直角三角形から、ＡＤ＝２ＥＤ 　ＡＤ＝ＤＦ、またＤＦ＝ＤＣから、 　△ＤＡＣはＡＤ＝ＤＣの二等辺三角形 　∠ＤＣＡ＝５０ 　　　　　　　　　　　　答え　∠ＡＣＢ＝５０°

上の証明から、四角形ＡＢＦＤに注目すれば、問題（１０，２０，８０，２０）や、この問題９の類題として（２０，１０，７０，４０）、（２０，４０，３０，１０）等が解決します。

　　　　　

［問題３４　の解答］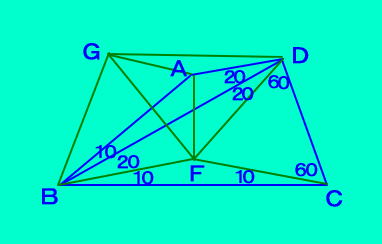

△ＢＤＣの外心をＦとすると、 　ＦＢ＝ＦＧ＝ＦＣ 　　　△ＤＦＣは正三角形 　△ＡＢＦをＡＢで折り返し、Ｆ→Ｇとする。 　∠ＡＢＦ＝３０より、△ＦＢＧは正三角形で、 　直線ＡＢはＧＦの垂直2等分線 　△ＧＦＤは点Ｆのまわりの角度から、 　頂角８０°の二等辺三角形。 　∠ＡＤＦ＝４０＝∠ＧＦＤ／２ 　以上から、定理６より、 　ＡＦは∠ＧＦＤの2等分線 　∠ＡＦＤ＝∠ＡＤＦ 　四角形ＡＦＣＤはたこ形で 　ＡＣはその対称軸 　　　　答え　∠ＡＣＢ＝４０°

[問題３５の答え］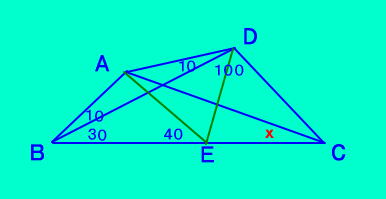

辺ＢＣ上に∠ＡＥＢ＝４０となる点Ｅをとると。 　△ＡＢＥは二等辺三角形、 　△ＡＢＤも二等辺三角形より、 　点Ａは△ＢＥＤの外心、∠ＢＤＥ＝５０　から、 　△ＡＥＤは正三角形 　以上から　∠ＤＥＣ＝８０、∠ＥＤＣ＝５０ 　△ＥＤＣも二等辺三角形　ＥＤ＝ＥＣ 　△ＡＥＣは二等辺三角形 　　　　答え　∠ＡＣＥ＝２０°

問題の類題として　（５０，３０，８０，５０）　、（７０、３０、７０、７０）があります。

［問題４０の答え］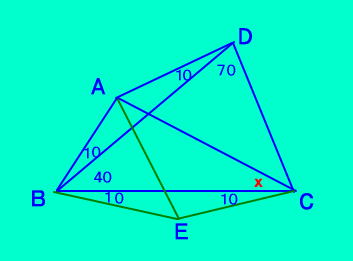

△ＡＢＤ、△ＢＤＣは二等辺三角形である。 △ＡＢＤをコピーして辺ＢＣに図のように 貼り付けると△ＡＢＥは正三角形 　ＡＢ＝ＡＥ＝ＢＥ＝ＥＣ △ＡＥＣは二等辺三角形よって 　∠ＡＥＣ＝∠ＢＥＣ−∠ＢＥＡ 　　　　　　＝１６０−６０＝１００ 　∠ＡＣＥ＝（１８０−１００）／２ 　　　　　　＝４０ 　　　　答え　∠ＡＣＢ＝３０°

［問題６９の答え］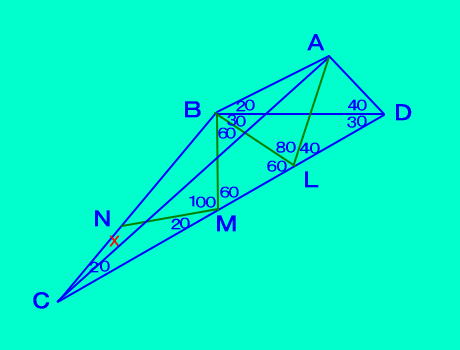

△ＡＢＤの外心はＤＣ上にあり、点Ｌとする。 　ＣＤ上に∠ＤＢＭ＝９０となる点Ｍをとる。 　ＣＢ上に∠ＣＭＮ＝２０となる点Ｎをとる。 　それぞれの二等辺三角形から、 　ＬＤ＝ＬＡ＝ＬＢ＝ＬＭ＝ＭＢ＝ＭＮ＝ＮＣ 　ここで、△ＮＣＭと△ＬＭＡは 　頂角１４０の合同な二等辺三角形 　よって、ＭＣ＝ＭＡ 　頂角１６０の二等辺三角形ＭＡＣから、 　∠ＭＣＡ＝１０ 　　　答え　∠ＡＣＢ＝１０°